Ciało Doskonale Czarne (CDC) to z definicji obiekt, który pochłania całe promieniowanie, które na niego pada, wliczając w to zarówno światło widzialne, jak i inne zakresy promieniowania elektromagnetycznego. Jednak jego specjalne właściwości się na tym nie kończą. Okazuje się, że CDC emituje własne promieniowanie, którego widmo zależy wyłącznie od temperatury ciała, a nie od materiału, z którego jest zbudowane. Co za tym idzie, w miarę łatwo określić temperaturę takiego obiektu dzięki znajomości widma jego promieniowania.

Modele Ciała Doskonale Czarnego

Jak to często bywa w fizyce, idealne modele nie istnieją w rzeczywistości i podobnie jest z ciałem doskonale czarnym. Istnieją obiekty, które pochłaniają znaczną część promieniowania, ale nigdy nie jest to 100%. Jednakże można w bardzo prosty sposób stworzyć model takiego obiektu. Wystarczy zrobić niewielki otworek w szczelnym pudełku.

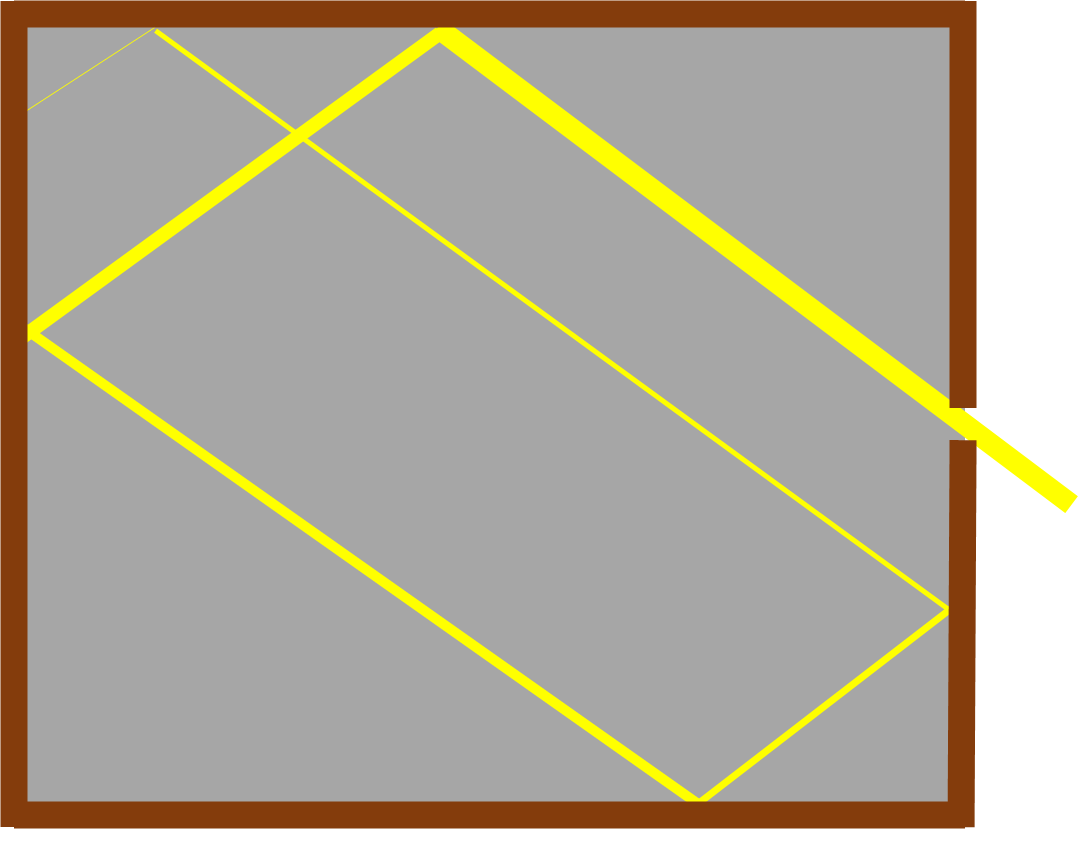
Światło wpada do wnętrza pudełka i zostaje pochłonięte przez jego ścianki. Dlatego wykonany otworek może być traktowany jak CDC, gdyż całe światło, które przez niego przeszło zostało pochłonięte w środku pudełka. Jeżeli ścianki pudełka są dodatkowo pokryte np. sadzą, model jest jeszcze dokładniejszy. Tego typu modele możemy zobaczyć także na co dzień. Gdy w środku dnia patrzymy w okna budynków, pomieszczenia w środku wydają się być bardzo ciemne. Dzieje się tak dlatego, że bardzo niewielka część światła dziennego wydostaje się z budynku przez okna.

Jeszcze lepszym modelem CDC są źrenice oczu. Światło, które wpada do oka przez źrenicę, zostaje pochłonięte we wnętrzu oka, więc nie wydostaje się na zewnątrz. Jedynie, przy bardzo gwałtownych zmianach naświetlenia, np. przy użyciu lampy błyskowej w aparatach fotograficznych, można zauważyć światło odbite od siatkówki. Zjawisko to znane jest pod nazwą efektu czerwonych oczu.

Z astronomicznego punktu widzenia, CDC jest bardzo ważnym modelem, z którego korzysta się do badania gwiazd. Gwiazdy także są w przybliżeniu doskonale czarne. Znając rozkład promieniowania gwiazdy, można więc obliczyć jej temperaturę.

Rozkład promieniowania

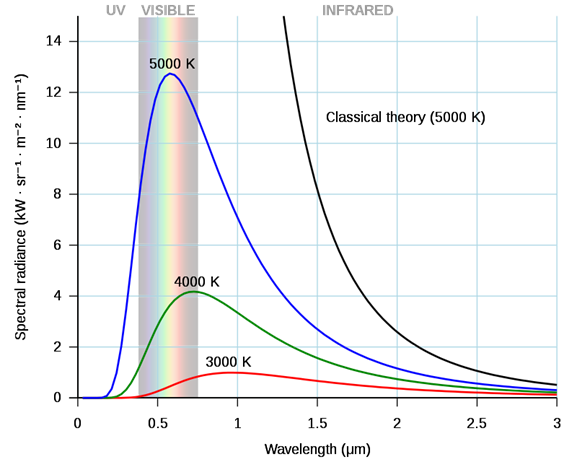
Pomimo znajomości rozkładu promieniowania, przez wiele lat nie udawało się go ująć formułą matematyczną. W XIX wieku fizyk John Rayleigh oraz astronom James Jeans próbowali wyprowadzić wzór na rozkład promieniowania CDC na gruncie ówczesnej termodynamiki. Jednak podejście to zakończyło się porażką. Według uzyskanego wzoru ciała powinny promieniować niezwykle intensywnie w zakresie fal o krótkiej długości, co nie zgadzało się z obserwacjami. Wynik uzyskany przez Rayleigha i Jeansa został nazwany „Katastrofą w nadfiolecie”. Matematyczny opis rozkładu próbował również uzyskać Wilhelm Wien na podstawie danych empirycznych. Rozkład Wiena znacznie lepiej opisywał promieniowanie CDC, jednak nadal występowały odstępstwa od danych doświadczalnych oraz brakowało teorii opisującej to zjawisko.

Zarówno poprawny wzór na rozkład promieniowania CDC, jak i teorię go opisującą dostarczył Max Planck w 1900 roku. Planck założył, że energia jest skwantowana, tj. może być pochłaniana i wypromieniowywana jedynie ściśle określonymi porcjami. Z pomocą tego założenia Planck wyprowadził rozkład w pełni zgadzający się z danymi empirycznymi.

Darth Kule

Pomimo że sama krzywa opisująca rozkład ma skomplikowaną matematyczną budowę, jej maksimum jest znacznie prostsze do opisania. To właśnie maksimum najczęściej używa się do badania temperatury gwiazd. Jak można zauważyć na grafice, wraz ze wzrostem temperatury, maksimum przesuwa się w kierunku krótszych długości fal.

Zależność pomiędzy położeniem maksimum a temperaturą opisuje prawo Wiena:

Gdzie stała Wiena . Dla temperatur około 2500-3000 K otrzymujemy maksimum , które leży w zakresie promieniowania podczerwonego. Taką temperaturę uzyskiwały m.in. żarówki z włóknem wolframowym.

Inną wartością, którą można w łatwy sposób odczytać z rozkładu promieniowania CDC jest zależność mocy źródła promieniowania od jego temperatury. CDC o wyższej temperaturze emitują większą ilość energii w czasie. Matematycznie tę zależność opisuje prawo Stefana-Boltzmanna:

Gdzie stała Stefana-Boltzmanna . to moc źródła podzielona przez jego pole powierzchni. Oznacza to, że ciało o powierzchni S w czasie t wypromieniuje energię równą:

Przykładowe zadania

1. Mikrofalowe promieniowanie tła jest najstarszą znaną pozostałością po Wielkim Wybuchu. Okazuje się, że jego rozkład promieniowania doskonale odpowiada rozkładowi dla Ciała Doskonale Czarnego. Jakiej temperaturze odpowiada ten rozkład, jeżeli jego maksimum przypada dla fali o częstotliwości 282 GHz
2. Moc promieniowania słonecznego, padającego prostopadle na powierzchnię Ziemi, wynosi ok. 1361 W/m². Przyjmując, że Słońce jest ciałem doskonale czarnym, oblicz temperaturę powierzchni Słońca oraz długość fali świetlnej, dla której przypada maksimum emisji, wiedząc, że promień Słońca wynosi ok. 6,96∙10⁸ m, a odległość z Ziemi do Słońca 1,5∙10¹¹ m.
3. Rozważmy dwa obiekty: (a) metalową sferę o promieniu R i temperaturze T_a = 300 K oraz (b) „podziurawioną” sferę otrzymaną z takiej samej sfery jak (a), poprzez wywiercenie w niej niewielkich otworków o promieniach dużo mniejszych niż R, ale dużo większych niż grubość sfery. Powierzchnia wyciętych otworów jest równa połowie powierzchni początkowej sfery. Jaką temperaturę T_b musi mieć sfera (b), aby jej moc promieniowania była równa mocy wydzielanej przez sferę (a)? Przyjmij, że sfery są ciałami doskonale czarnymi oraz pomiń fakt, że długości niektórych fal emitowanych przez sfery są większe od wielkości otworów.

Rozwiązania

Zadanie 1

Aby rozwiązać to zadanie, należy skorzystać z prawa Wiena.

Znając częstotliwość i prędkość fali, możemy znaleźć jej długość:

Podstawiając częstotliwość z zadania i prędkość światła w próżni otrzymamy wynik około 2,72 K.

Zadanie 2

Pierwszym krokiem jest policzenie mocy promieniowania emitowanego przez Słońce. Aby je znaleźć, należy pomnożyć moc promieniowania padającego na metr kwadratowy razy całą powierzchnię, przez którą przejdzie promieniowanie. Ziemia znajduje się w odległości R_Z od Słońca, więc całe promieniowanie przechodzi przez sferę o promieniu R_Z. Wartość podana w zadaniu: 1361 to tzw. „stała słoneczna” i będzie oznaczana jako G_SC.

Znając moc promieniowania oraz promień Słońca R_S można, korzystając z prawa Stefana-Boltzmanna, wyznaczyć temperaturę powierzchni Słońca:

Podstawiając dane do wzoru otrzymujemy wartość T≈5780 K. Znając temperaturę powierzchni można, przy użyciu prawa Wiena, obliczyć długość fali świetlnej, dla której przypada maksimum emisji Słońca.

Długość ta wynosi ok. 500 nm i znajduje się przedziale odpowiadającemu światłu zielonemu.

Oczywiście w rzeczywistości powierzchnia Słońca nie ma jednolitej temperatury, a więc również maksimum emisji nie jest stałe, jednak zawsze znajduje się w okolicach barwy zielonej 490-570 nm.

Zadanie 3

Powierzchnia sfery (a) wynosi S_a=4πR². Korzystając z prawa Stefana-Boltzmanna można obliczyć moc wydzielaną przez tę sferę:

Powierzchnia obiektu (b) jest dwa razy mniejsza, czyli S_b=2πR². Jednakże w wypadku drugiego obiektu należy rozważyć również wewnętrzną powierzchnię, gdyż część promieniowania może uciec z wnętrza sfery przez otworki. Wydrążenia stanowią połowę powierzchni sfery, więc połowa energii wypromieniowanej przez wewnętrzną powierzchnię nie zostanie ponownie pochłonięta i zwiększy całkowitą moc promieniowania ciała (b).

Teraz należy przyrównać obydwie moce i z otrzymanego równania wyznaczyć temperaturę ciała (b):

Podstawiając dane z zadania, otrzymamy wynik około 322,37 K.