II Olimpijska Liga Astronomiczna: Zadanie 5 z 6 serii

Treść

Soczewkowanie grawitacyjne zostało przewidziane przez Einsteina 4 lata przed ogłoszeniem Ogólnej Teorii Względności w pracy „Trageser, W., von Meyenn, K., & Einstein, A. (1911). Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes”. Praca ta rozważa obiekt o dużej masie, który zagina trajektorię światła i w efekcie zachowuje się jak klasyczna soczewka. Potwierdzenie istnienia tego zjawiska zostało przedstawione przez Sir Arthura Stanleya Eddingtona dopiero w 1919 roku po wcześniejszych, nieowocnych próbach innych zespołów oraz poprawce Einsteina do swoich przewidywań.
Albert początkowo używał dosyć mocnych przybliżeń, a że warto go naśladować w niektórych kwestiach, to rozważmy obiekt o sferycznej symetrii i masie $M$ działający jak soczewka. Parametr rozpraszania (impact parameter) oznaczamy jako $\xi$ i mierzymy od środka obiektu. Równanie opisujące kąt zagięcia wiązki światła w tym przypadku ma postać:

$\varphi = \frac{4GM}{\xi c^2}$

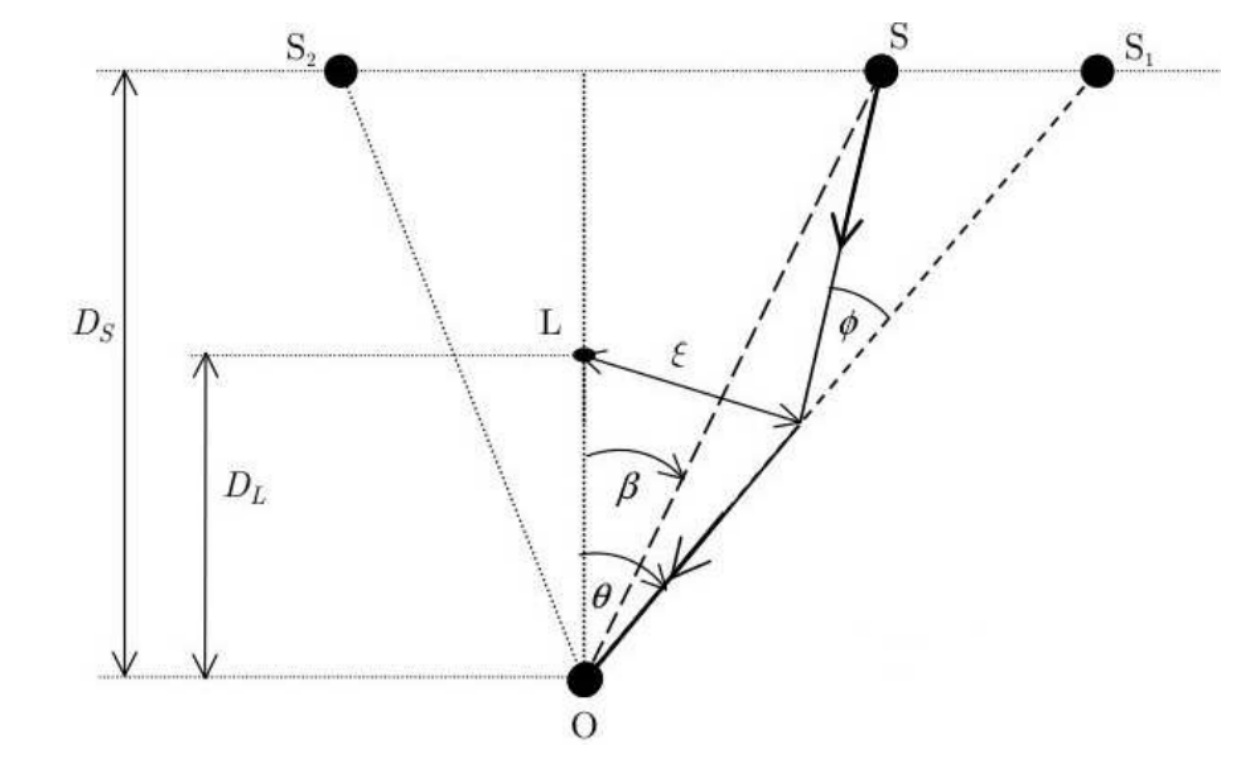
W uproszczonym modelu parametr rozpraszania można traktować jako najkrótszą odległość między środkiem soczewki a przebiegiem danej wiązki światła. Na rysunku 2 masywny obiekt (działający jak soczewka) znajduje się w punkcie L. Promienie świetlne emitowane przez źródło S, ugięte przez soczewkę, są obserwowane przez obserwatora O jako obrazy $S_1$ i $S_2$ . Przyjmujemy, że kąty $\varphi$ , $\beta$ oraz $\theta$ są bardzo małe.

(a) Dla szczególnego przypadku, w którym źródło jest idealnie ustawione względem soczewki (tj. $\beta = 0$ ), pokaż, że powstaje obraz w postaci pierścienia o promieniu kątowym, zwanym promieniem Einsteina $\theta_E$ , danego wzorem

$\theta_E = \sqrt{\frac{4GM}{c^2} \frac{D_S - D_L}{D_L D_S}}$

(b) Odległość Ziemi od gwiazdy wynosi około 50 kpc. Soczewka o masie jednego Słońca, znajdująca się na linii obserwacji jest oddalona od gwiazdy o 10 kpc. Oblicz promień kątowy pierścienia Einsteina utworzonego przez tę soczewkę zakładając, że Ziemia, gwiazda i środek geometryczny soczewki są ustawione w jednej linii.

(c) Podaj rozdzielczość teleskopu kosmicznego Hubble’a (średnica lustra – 2,4 m) . Czy jest on w stanie zaobserwować pierścień Einsteina z punktu (b)?

(d) Na rysunku 2, dla izolowanego punktowego źródła S, soczewka grawitacyjna tworzy dwa obrazy $S_1$ oraz $S_2$ . Znajdź ich pozycje ( $\theta_1$ i $\theta_2$ ), a odpowiedź wyraź w zależności od $\beta$ oraz $\theta_E$ .

(e) Znajdź stosunek $\theta_{1,2}/\beta$ (tj. $\theta_1/\beta$ lub $\theta_2/\beta$ ) w zależności od $\eta$ . $\theta_{1,2}$ oznacza tutaj każdą z pozycji obrazów z punktu (d), a $\eta$ wyraża stosunek $\beta/\theta_E$ .

(f) Znajdź wartości powiększeń $\Delta \theta/\Delta \beta$ w zależności od $\eta$ dla $\theta = \theta_{1,2}$ (tj. dla $\theta = \theta_1$ lub $\theta = \theta_2$ ), przy założeniu, że $\Delta \beta \ll \beta$ oraz $\Delta \theta \ll \theta$ .

Autor: Rafał Bryl

Rozwiązanie

Zaczniemy od ogólnego rozwiązania $\beta \neq 0$ , a następnie przejedziemy do przypadku szczególnego $\beta = 0$ . Zauważmy, że $\phi$ , $\beta$ , i $\theta$ są małymi kątami, więc punkt załamania znajduje się blisko soczewki i w dobrym przybliżeniu odległość miedzy nim, a obserwatorem wynosi $D_L$

(1) $\begin{align*} PS &= PS + SS_1 \\ \theta D_S &= \beta D_S + (D_S - D_L)\phi \\ (\theta - \beta)D_S &= (D_S - D_L)\frac{4GM}{c^2} \frac{1}{D_L} = \frac{4GM}{c^2} \frac{(D_S - D_L)}{D_L} \\ \theta(\theta - \beta) &= \frac{4GM}{c^2} \frac{(D_S - D_L)}{D_L D_S} \\ \theta^2 - \beta\theta &= \frac{4GM}{c^2} \frac{(D_S - D_L)}{D_L D_S} \end{align*}$

(a) Dla $\beta = 0$ , mamy $\theta = \pm \theta_E$ , gdzie

(2) $\begin{equation*} \theta_E = \sqrt{ \frac{4GM}{c^2} \frac{(D_S - D_L)}{D_L D_S} } \end{equation*}$

(b) Dla danych wartości:

(3) $\begin{align*} D_L &= 50 - 10 = 40 \text{kpc} \\ \theta_E &= \sqrt{ \frac{4GM}{c^2} \frac{(D_S - D_L)}{D_L D_S} } \\ \theta_{E1} &= \sqrt{ \frac{4 \times 6,672 \times 10^{-11} \times 1,989 \times 10^{30} \times (50 - 40)}{(3 \times 10^8)^2 \times 50 \times 40 \times 3,0856 \times 10^{19}} } \\ &= 9,8 \times 10^{-7} \text{rad} \\ \theta_{E1} &= 2,0 \times 10^{-4} \text{arcsec} \end{align*}$

(4) $\begin{align*} \theta_{Hubble} &= \frac{1,22 \lambda}{D} = 1,22 \times \frac{5 \times 10^{-7}}{2,4} \\ &= 2,5 \times 10^{-7} \text{rad} \\ \theta_{Hubble} &> \theta_{E1} \end{align*}$

Teleskop Hubble’a nie może zaobserwować dobrze tego pierścienia Einsteina.

(d) Równanie kwadratowe daje nam dwa różne pierwiastki:

(5) $\begin{align*} \theta_1 &= \frac{\beta}{2} + \sqrt{ \left( \frac{\beta}{2} \right)^2 + \theta_E^2 } \\ \theta_2 &= \frac{\beta}{2} - \sqrt{ \left( \frac{\beta}{2} \right)^2 + \theta_E^2 } \end{align*}$

Oznacza to, że zaobserwujemy dwa obrazy dla pojedynczego źródła

(e) Dzieląc równania z punktu (d) przez $\beta$ :

(6) $\begin{align*} \frac{\theta_{1,2}}{\beta} &= \frac{1}{2} \pm \sqrt{ \left( \frac{1}{2} \right)^2 + \left( \frac{\theta_E}{\beta} \right)^2 } \\ &= \frac{1}{2} \left( 1 \pm \sqrt{1 + \frac{4}{\eta^2}} \right) \quad \end{align*}$

gdzie $\eta = \frac{\beta}{\theta_E}$

Zatem:

(7) $\begin{align*} \left[ \frac{\Delta \theta}{\Delta \beta} \right]_{\theta = \theta_{1,2}} &= \frac{\theta}{2\theta - \beta} \\ &= \frac{\theta_{1,2}}{2\theta_{1,2} - \beta} \\ &= \frac{\theta_{1,2}/\beta}{2\theta_{1,2}/\beta - 1} \\ &= \frac{ \left( \frac{1}{2} \left( 1 \pm \sqrt{1 + \frac{4}{\eta^2}} \right) \right)}{ \left( 2 \left( \frac{1}{2} \left( 1 \pm \sqrt{1 + \frac{4}{\eta^2}} \right) \right) - 1 \right) } \\ &= \frac{ \eta \pm \sqrt{\eta^2 + 4} }{ 2(\eta \pm \sqrt{\eta^2 + 4} - \eta) } \\ &= \frac{1}{2} \left( 1 \pm \frac{\eta}{\sqrt{\eta^2 + 4}} \right) \end{align*}$

Zadanie pochodzi z Olimpijskiej Ligi Astronomicznej. Więcej informacji o konkursie i o obecnej edycji można znaleźć na stronie: https://almukantarat.pl/liga-astronomiczna/.

Korekta – Zofia Lamęcka

Treść

Rozwiązanie

II Olimpijska Liga Astronomiczna: Zadanie 3 z 5 serii

II Olimpijska Liga Astronomiczna: Zadanie 1 z 4 serii

II Olimpijska Liga Astronomiczna: Zadanie 4 z 3 serii

II Olimpijska Liga Astronomiczna: Zadanie 1 z 1 serii