Wyobraźmy sobie ogromny obłok materii, z którego powstanie w przyszłości gwiazda. Głównym jego składnikiem jest wodór, będący najpowszechniejszym pierwiastkiem we Wszechświecie. Jeżeli nie byłoby w jego otoczeniu żadnych silnych źródeł energii jak na przykład gwiazdy, to ruch wewnątrz zimnej, gazowej struktury nastąpi pod wpływem sił grawitacyjnych między cząsteczkami. Wygląda więc na to, że obłok taki posiada jakąś energię mechaniczną. Postaramy się ją opisać.
Autorem artykułu jest Jurand Prądzyński.
Energia grawitacyjna
Suma energii kinetycznych cząsteczek takiego obłoku, na podstawie klasycznej definicji energii możemy zapisać jako:
(1)
Wynika stąd, że przy założeniu o jednorodności cząstek gazu, całkowita masa równa się masie cząstek gazu przemnożonej przez liczbę tych cząstek . Pomnóżmy więc równanie (1) przez
:
(2)
Wyrażenie w ostatnim nawiasie jest znaną nam z matematyki średnią kwadratową. Nazwijmy więc ten parametr średnią prędkością kwadratową (RMS to skrót od angielskiego root mean square velocity). Okazuje się być to bardzo użyteczne w korelacji z inną, znaną, makroskopową wartością — temperaturą. Przypomnijmy, że jest ona miarą średniej kinetycznej energii. Zapiszmy więc równanie energii cząstek obłoku:
gdzie to liczba stopni swobody cząstek, a
– stała Boltzmanna.
Załatwiliśmy więc sprawę energii kinetycznej obłoku. Pozostaje spróbować opisać jego energię potencjalną.
Przypomnijmy sobie jak wyrazić energię potencjalną układu trzech gwiazd równoodległych od siebie. Grawitacyjna energia potencjalna układu, względem inercjalnego obserwatora, to praca, jaką należy wykonać, aby z nieskończoności przenosić kolejne gwiazdy do ustalonych położeń. Jaką więc należy wykonać pracę, aby przenieść z nieskończoności jedną gwiazdę o masie ? Żadną. Aby zrobić to samo z drugą, identyczną gwiazdą, na odległość
od tej pierwszej, potrzebna jest nam praca odpowiadająca energii potencjalnej
, natomiast dla trzeciej gwiazdy to już
.
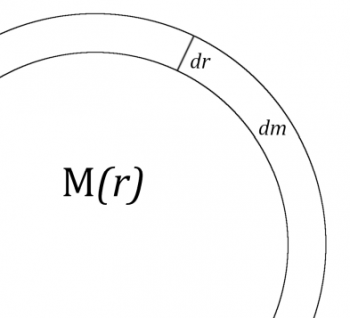
Podobne rozumowanie wykorzystamy do problemu energii obłoku materii. Załóżmy więc dla uproszczenia, że obłok jest sferyczny i ma promień . Przeniesienie cząstki o masie
z nieskończoności na jego powierzchnię wymaga energii
. Poprzez
oznaczyliśmy tutaj masę zgromadzoną we współśrodkowej z gwiazdą kuli o promieniu
. Uznajmy, że
jest na tyle małe, że bez strat ogólności rozumowania w jego objętości gęstość jest stała. Wtedy:
gdzie to powierzchnia
. Nakładając na obłok całą sferę o grubości
otrzymujemy:
Zapiszmy teraz, jakiej energii potrzebujemy do przeniesienia z nieskończoności. Przyjmiemy, że
– na ogół jest to złe założenie i w zależności od wielu czynników przyjmuje się różne rozkłady gęstości w rozpatrywanych obłokach, jednakże aby pokazać jak matematycznie działa ten model wystarczy nam tylko ten przypadek, będący rachunkowo dość prosty. Mamy:
Całkując obustronnie powyższe równanie dostajemy:
(3)
oznaczamy promień obłoku. Właśnie wyznaczona wartość
nazywana jest energią grawitacyjną. Jest to suma energii potencjalnych składników układu.
Warto wspomnieć jeszcze o jednej kwestii. Uwzględniliśmy dla energię potencjalną wyłącznie względem masy o mniejszej, lub takiej samej odległości względem środka obłoku niż
. Możemy jednak łatwo się przekonać, że to całkowicie wystarczy, stosując wniosek z prawa Gaussa o stałości potencjału grawitacyjnego wewnątrz sferycznej powłoki.
Aby połączyć energię grawitacyjną obłoku z jego energią kinetyczną, wykorzystamy (bez dowodu) twierdzenie Clausiusa o wiriale mówiące w tym przypadku, że dla momentu bezwładności wyznaczonego względem pewnej osi przechodzącej przez środek obłoku prawdziwa jest równość:
W szczególności, gdy obłok nie ulega implozji, ani ekspansji zewnętrznych warstw, czyli gdy , mamy:
co po wstawieniu wyznaczonych w (2) i (3) równań daje nam:
Równowaga hydrostatyczna
W astrofizyce szczególnie ważnym zjawiskiem jest równowaga między wewnętrznym parciem gazu, a siłą grawitacji ściskającą obłok. Stan ten nazywamy równowagą hydrostatyczną. Główną przyczyną powstawania ciśnienia jest ruch gazu wewnątrz obłoku. Drugą przyczyną, w przypadku gorących obłoków takich jak gwiazdy, jest ciśnienie promieniowania. Postaramy się opisać matematycznie mechanizm powstawania równowagi hydrostatycznej.
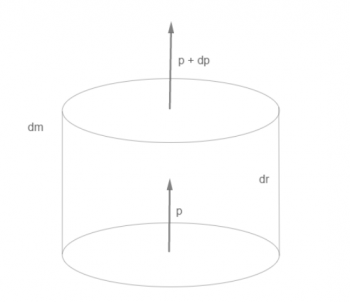
Niech ciśnienie oznaczone będzie jako . Rozpatrzmy więc cylindryczną, bardzo małą masę
wewnątrz obłoku, w odległości
od jej promienia. Podstawy obiektu skierowane są prostopadle do kierunku na środek obłoku i mają pole
. Wysokość takiego walca to
.
Zauważmy, że na podstawę znajdującą się bliżej centrum obłoku działa większa siła grawitacji. Wynika to z faktu, że nacisk poza dalszymi warstwami wywiera również samo . Mamy:
gdzie to siła od warstwy sponad rozważanego cylindrycznego walca. Mamy:
Odejmując stronami oba powyższe równania dostajemy:
Opiszemy teraz element siły . Część obłoku pod walcem jest sferyczna, a samo rozpatrywane
bardzo małe, stąd:
Dalej więc, z prawa powszechnego ciążenia:
Siłę zapisaliśmy ze znakiem minus, ze względu na opis ciśnienia, które jest skierowane przeciwnie do działania siły grawitacji. Ostatecznie więc jako funkcja odległości opisywana jest przez:
(4)
Wynik ten nosi nazwę równania równowagi hydrostatycznej gwiazdy i jest jednym z najważniejszych opisujących termodynamiczne parametry gwiazdy.
Zadania
- Średnia gęstość Ziemi wynosi
. Oszacuj wartość ciśnienia
w środku Ziemi. Przyspieszenie ziemskie (na jej powierzchni) wynosi
, a promień Ziemi
. Źródło: ZF-956, magazyn Delta
- Oszacuj masę gwiazd w gromadzie kulistej o promieniu
i średniej prędkości kwadratowej gwiazd w gromadzie
. Źródło: III IOAA, Iran.
- Grawitacyjna energia własna ciała o kształcie kulistym wyraża się wzorem:
gdzie
jest współczynnikiem zależnym od radialnego rozkładu gęstości w ciele,
– stałą grawitacji,
– masą ciała, a
– jego promieniem.
Przyjmując, że obecnie Słońce ma masę, promień
i temperaturę efektywną
oraz, że dla Słońca
, oblicz ile wynosiłby promień Słońca po upływie
lat, gdyby jedynym źródłem jego energii było grawitacyjne kurczenie się, a emisja była taka sama i odpowiadała obecnej mocy promieniowania Słońca. Źródło: Zadanie 2 zawodów III stopnia XXVII OA.
Rozwiązania
Zadanie 1
Przyjmujemy założenie, że Ziemia jest jednolitą bryłą. Mamy wtedy całkując równanie równowagi hydrostatycznej gwiazdy:
a ponieważ na zewnątrz ciśnienie wynosi stale 0, to i
Zadanie 2
Łatwo możemy zauważyć, że wyprowadzona przez nas teoria nie tyczy się tylko cząsteczek gazu, ale również jest prawdziwa dla wielu obiektów makroskopowych poddających się działaniu sił grawitacji. Mamy na mocy twierdzenia o wiriale:
Zadanie 3
Opisany wyżej współczynnik wprowadza się, aby określić dla innych niż stały rozkładów
, energię grawitacyjną
, gdzie
i
.
Różnica energii potencjalnych w czasie i
odpowiada zgodnie z hipotezą energii wypromieniowanej, czyli
, gdzie
to moc promieniowania Słońca. Z prawa Stefana-Boltzmanna mamy:
Mamy więc:
jest szukaną wartością. Wobec tego: