Mechanika nieba 2: Pole grawitacyjne

Posted on 23 czerwca 202124 maja 2021 by Radosław Kubiś 5k odsłon

Kiedy Isaac Newton opisał swoje Prawo Powszechnego Ciążenia, stanął przed pewnym problemem. Obiekty oddziałują ze sobą, nie mając bezpośredniego kontaktu. Newton nie był w stanie zrozumieć skąd masy „wiedzą”, że powinny się przyciągać. Na pytanie to częściowo odpowiada wprowadzone później pojęcie pola siły.

Pole grawitacyjne i natężenie pola

Istnienie w przestrzeni masy oznacza, że możemy wprowadzić w tej przestrzeni pole grawitacyjne, z którym mogłyby oddziaływać inne masy. Aby wyobrazić sobie, jak takie pole może wyglądać, umieśćmy w pobliżu masy M masę próbną m. Masa próbna to masa na tyle mała, że nie wpływa znacząco na układ, w którym ilustrujemy pole grawitacyjne. Teraz zaznaczmy tory, po których będzie się poruszać masa próbna m. Są to tak zwane linie pola.

Jednak do lepszego opisu pola niezbędna jest jakaś wielkość mierzalna, a nie tylko ładny rysunek. W pierwszym odruchu wydaje się, że dobrą wartością do opisu pola sił, jest siła pochodząca od tego pola w danym punkcie. Jednak, jak wiadomo z równania Newtona, siła ta będzie różna, dla różnych obiektów.

Uniezależnijmy więc siłę od masy próbnej. Aby to zrobić, zwyczajnie podzielmy siłę przez masę. Uzyskana w ten sposób wielkość to natężenie pola grawitacyjnego zapisywana zazwyczaj jako $\vec {\gamma}$ , jest to wektor o tym samym kierunku i zwrocie, co siła działająca na masę próbną i jest wyrażona wzorem:

$\vec {\gamma} = \frac {\vec{F}} {m}$

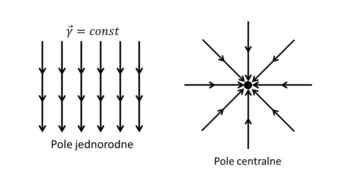
Jednostką natężenia pola grawitacyjnego jest $\frac {m} {s^2}$ . Należy zwrócić uwagę, że kierunek natężenia pola jest zawsze styczny do linii pola. Ze względu na natężenie możemy rozróżnić kilka rodzajów pól, w tym pole jednorodne i pole centralne.

Radosław Kubiś

W każdym punkcie pola jednorodnego natężenie jest takie samo (zarówno co do wartości, kierunku, jak i zwrotu). W przybliżeniu takie pole występuje m.in. na powierzchni Ziemi, a jego natężenie wynosi ok. 9,81 $\frac {m} {s^2}$ , czyli tyle samo, co przyspieszenie grawitacyjne $\vec {g}$ . Nie jest to przypadek, ponieważ dla pola grawitacyjnego natężenie odpowiada przyspieszeniu działającemu na masę próbną w danym punkcie.

W polu centralnym wszystkie linie pola są półprostymi zbiegającymi się do wspólnego centrum. Taką formę przyjmuje pole grawitacyjne dla pojedynczej masy. Natężenie ma wtedy postać:

$\vec {\gamma} = -\frac {\vec{F}} {m} = -\frac {GMm} {r^2m} \hat{r} = \frac {GM} {r^2} \hat {r}$

$\hat {r}$ zawiera informacje o kierunku i zwrocie pola, jest to wektor długości jeden i tym samym kierunku co $\vec {F}$ .

Ważną właściwością pól jest superpozycja. Oznacza ona, że natężenie pola pochodzącego od wielu mas jest sumą wektorową natężeń każdego z pól składowych. Dlatego dla układu mas jesteśmy w stanie zawsze sprowadzić pole grawitacyjne do sumy kilku pól centralnych.

Energia potencjalna i potencjał grawitacyjny

Siła grawitacji jest siłą zachowawczą, co znaczy, że praca wykonana przez nią przy przemieszczaniu ciała jest zależna wyłącznie od położenia początkowego i końcowego ciała, nie zaś od pokonanej drogi. Zatem można zdefiniować dla niej energię potencjalną. Ponadto pole grawitacyjne jest polem centralnym, energia potencjalna będzie więc zależeć jedynie od odległości obiektu od centrum. Przyjmijmy również, że energia potencjalna będzie wynosić 0 w bardzo dużej (czyli w dążącej do nieskończoności) odległości od centrum. W ten sposób wzór na energię potencjalną w polu grawitacyjnym przyjmujący postać: $E_p = -\frac {GMm} {r}$ . Tak zdefiniowana energia potencjalna będzie zawsze ujemna.

Zwróćmy jednak uwagę, że podobnie, jak w wypadku siły, energia potencjalna przyjmuje różną wartości, dla różnych mas próbnych. Zastosujmy więc wobec niej ten sam trik, co dla siły i podzielmy energię potencjalną przez masę obiektu. Otrzymana w ten sposób wielkość nazywana jest potencjałem grawitacyjnym i zapisywana za pomocą symbolu $\phi$ . Jednostką potencjału jest $\frac {J} {kg} = \frac {m^2} {s^2}$ .

$\phi = \frac {E_p} {m} = -\frac {GMm} {rm} = -\frac {GM} {r}$

W ten sposób otrzymaliśmy drugą wielkość służącą do opisu pola grawitacyjnego. Potencjał jest jednak prostszy w użyciu od natężenia, ponieważ jest skalarem, czyli liczbą. Oznacza to, że zgodnie z zasadą superpozycji pól możemy obliczyć potencjał grawitacyjny w danym punkcie, dodając potencjały pól składowych, nie przejmując się wektorem natężenia.

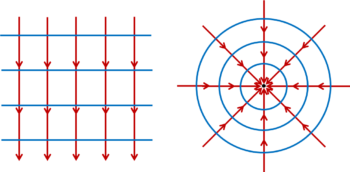
Znajdźmy teraz wszystkie punkty, w których potencjał przyjmuje jedną, określoną wartość. Punkty te utworzą pewną powierzchnię w polu grawitacyjnym, którą nazywamy powierzchnią ekwipotencjalną. Na dwuwymiarowym rysunku przyjęłaby postać krzywej. Warto zauważyć, że linie pola są zawsze prostopadłe do powierzchni ekwipotencjalnych.

Radosław Kubiś

Linie pola (czerwone) i powierzchnie ekwipotencjalne (niebieskie) dla pola jednorodnego i centralnego.

Potencjał może posłużyć do szybkiego wyliczania zmiany energii potencjalnej. Różnica potencjałów w dwóch punktach pomnożona przez masę obiektu, który przemieścił się między tymi punktami, jest równa zmianie jego energii potencjalnej.

$\Delta E_p = E_{p2} - E_{p1} = m \phi_2 - m \phi_1 = m \left (\phi_2 -\phi_1 \right)$

Prędkości kosmiczne

Przypuśćmy, że satelita okrąża planetę po idealnym okręgu o promieniu $r$ . Z jaką prędkością będzie poruszał się ten satelita? Wiadomo, że aby ciało poruszało się po okręgu, musi działać na nie siła dośrodkowa $F_d = \frac{mv^2}{r}$ . W naszym przypadku rolę siły dośrodkowej pełni siła grawitacji.

$\frac{GM\cancel{m}}{r^2} = \frac{\cancel{m}v^2}{r}$

Przy okazji warto zauważyć, że masa satelity się skraca, więc równie dobrze moglibyśmy przyrównywać natężenie pola grawitacyjnego do przyspieszenia dośrodkowego. Z tak sformułowanego równania należy teraz wyznaczyć $v$ .

$v = \sqrt{\frac{GM}{r}}$

W ten sposób wyprowadziliśmy równanie na prędkość satelity poruszającego się po okręgu. Prędkość ta nie zależy od masy satelity. Należy jednak pamiętać, że przy odpowiednio masywnym satelicie (np. Księżycu) będzie odległością od środka masy obydwu ciał, a nie od środka planety.

W szczególności, jeżeli do wzoru podstawimy masę i promień Ziemi, otrzymamy wartość $v_I \approx 7,91 \frac{km}{s}$ . Jest to tzw. pierwsza prędkość kosmiczna dla Ziemi. Do jej obliczenia został użyty promień Ziemi, więc jeśli chcielibyśmy obliczyć prędkość satelity na orbicie, należałoby podstawić promień orbity.

Teraz przypuśćmy, że chcemy wystartować rakietą z powierzchni Ziemi tak, aby na zawsze uciekła z jej pola grawitacyjnego. Tym razem do wyliczenia prędkości posłużymy się zasadą zachowania energii mechanicznej. Na powierzchni Ziemi rakieta ma pewną (ujemną) energię potencjalną oraz (po nadaniu prędkości) energię kinetyczną. Aby rakieta uciekła z pola grawitacyjnego musi mieć dostatecznie dużo energii, aby dolecieć do „nieskończoności”, czy też bardziej realnie do punktu, w którym energia potencjalna wyniesie 0. Chcemy uzyskać najmniejszą potrzebną prędkość, więc w tym punkcie ona również będzie dążyć do 0.

$-\frac{GM\cancel{m}}{r} + \frac{\cancel{m}v^2}{2} = 0 + 0$

Analogicznie do pierwszego przykładu masa rakiety się skraca. Również tym razem należy wyznaczyć $v$ z równania.

$v = \sqrt{\frac{2GM}{r}}$

Jeżeli teraz do tego wzoru podstawimy dane dla Ziemi, otrzymamy $v_{II} \approx 11,19 \frac{km}{s}$ . Jest to wartość drugiej prędkości kosmicznej dla Ziemi. Warto zwrócić uwagę na bardzo prosty związek pomiędzy tymi dwiema prędkościami.

$v_I = \sqrt{2}\cdot v_{II}$

Związek ten będzie prawdziwy dla dowolnego ciała. Należy jedynie pamiętać, że w prędkościach kosmicznych $r$ jest promieniem danego obiektu.

Przykładowe zadania

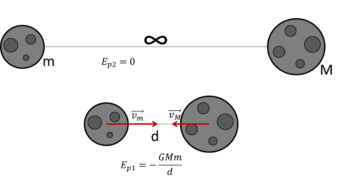
Dwie asteroidy o masach m i M początkowo znajdują się w bardzo dużej odległości, którą można traktować, jak nieskończoną. Następnie wskutek wzajemnego przyciągania zaczęły się zbliżać. Jaka była ich względna prędkość, gdy zbliżyły się na odległość d?
W jakiej odległości od Ziemi znajduje się punkt, w którym oddziaływania grawitacyjne Ziemi i Księżyca wzajemnie się znoszą? Jaką wartość ma potencjał grawitacyjny w tym punkcie?
Masa Ziemi wynosi 5,97 ∙ 10²⁴[kg], masa Księżyca 7,35 ∙ 10²²[kg], odległość między Ziemią a Księżycem 3,84 ∙ 10⁸[m], a stała grawitacyjna 6,67 ∙ 10^-11 [N∙m2/kg2].
Udowodnij, że natężenie pola grawitacyjnego we wnętrzu idealnej sfery, jest w każdym punkcie równe 0.

Rozwiązania

Zadanie 1

Ponieważ początkowo asteroidy znajdowały się bardzo daleko od siebie, ich energia potencjalna wynosiła E_p0=0. Gdy zbliżyły się do siebie ich energia potencjalna wynosiła $E_{p1} = -\frac {GMm} {d}$ .

Radosław Kubiś

Zgodnie z zasadą zachowania energii mechanicznej energia kinetyczna musiała wzrosnąć.

$E_{p0} + E_{k0} = E_{p1} + E_{k1}$

$(1) \quad 0 + 0 = -\frac {GMm} {d} + \frac {mv_m^2} {2} + \frac {Mv_M^2} {2}$

Prędkość względną uzyskamy, dodając prędkości obu asteroid:

$(2) \quad v = v_m + v_M$

Do pełnego rozwiązania brakuje tylko jednego równania, które uzyskamy z zasady zachowania pędu, gdyż na asteroidy nie działają żadne siły zewnętrzne.

$(3) \quad 0 = mv_m - Mv_M$

Ze wzoru (3) możemy wyliczyć v_m, podstawić je do równania (1) i wyliczyć v_M:

$v_m = \frac {M} {m} v_M$

$\frac {GMm} {d} = \frac {m} {2} \left (\frac {M} {m} v_M \right)^2 + \frac {Mv_M^2} {2}$

$\frac {2GMm} {d} = \frac {M^2} {m} v_M^2 + {M} v_M^2$

$\frac {2Gm^2} {d} = \left (M + m \right) v_M^2$

$(4) \quad v_M = m \sqrt {\frac {2G} {d \left (M + m\right)} }$

Zauważmy, że jeśli powtórzymy to samo dla v_m uzyskamy ten sam wynik z zamienionymi m i M:

$(5) \quad v_m = M \sqrt { \frac {2G} {d \left (M + m\right)} }$

Teraz możemy wartości z równań (4) i (5) podstawić do równania na prędkość względną (2):

$v = m \sqrt {\frac {2G} {d \left (M + m\right)} } + M \sqrt {\frac {2G} {d \left (M + m \right)} }$

$v = \left (M + m\right) \sqrt {\frac {2G} {d \left (M + m\right)} }$

$(6) \quad v = \sqrt {\frac {2G \left (M + m\right)} {d} }$

W ten sposób otrzymaliśmy szukany wzór.

Zadanie 2

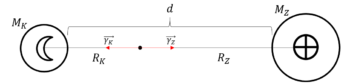
Łatwo zauważyć, że szukany punkt musi się znajdować na osi Ziemia-Księżyc pomiędzy nimi, gdyż tylko na tym odcinku natężenia pola grawitacyjnego Ziemi i Księżyca mają te same kierunki
i przeciwne zwroty, więc tylko tam ich suma może dawać 0.

Radosław Kubiś

Dzięki temu, że natężenia mają ten sam kierunek, ich dodanie jest bardzo proste, a ponieważ zwroty są przeciwne, wystarczy odjąć ich wartości. Dlatego też w równaniu (1) zostały uwzględnione jedynie wartości natężeń.

$(1) \quad \gamma_Z = \frac {GM_Z} {R_Z^2}, \quad \gamma_K = \frac {GM_K} {R_K^2}$

$(2) \quad d = R_Z + R_K$

$3) \quad \frac {GM_Z} {R_Z^2} - \frac {GM_K} {R_K^2} = 0$

Ze wzoru (3) można teraz obliczyć R_K:

$\frac {GM_Z} {R_Z^2} = \frac {GM_K} {R_K^2}$

$R_K^2 M_Z = R_Z^2 M_K$

$(4) \quad R_K = R_Z \sqrt {\frac {M_K} {M_Z} }$

Podstawiając R_K do wzoru (2) możemy znaleźć R_Z:

$d = R_Z + R_Z \sqrt {\frac {M_K} {M_Z} }$

$d = R_Z \left (1 + \sqrt {\frac {M_K} {M_Z} } \right)$

$(5) \quad R_Z = \frac {d} {1 + \sqrt {\frac {M_K} {M_Z} } }$

Na koniec wystarczy podstawić do wzoru (5) dane z zadania. Otrzymana odległość punktu, w którym oddziaływania grawitacyjne Ziemi i Księżyca się zerują, od Ziemi wynosi około 3,46 ∙ 10⁸[m].

Jak widać punkt ten znajduje się znacznie bliżej Księżyca niż Ziemi, co raczej nie dziwi. Nie należy mylić tego punktu, z pierwszym punktem Lagrange’a, który znajduje się w innym miejscu i uwzględnia dodatkowo siłę bezwładności.

Znając już położenie punktu, możemy obliczyć wartość potencjału grawitacyjnego. Wystarczy dodać do siebie potencjały od obu ciał.

$\phi = \phi_Z + \phi_K$

$(6) \quad \phi = -\frac {GM_Z} {R_Z} -\frac {GM_K} {R_K}$

Można wyliczyć R_K i podstawić je razem z R_Z bezpośrednio do (6), jednak, aby uzyskać bardziej ogólny wzór warto podstawić R_Z ze wzoru (5) i analogiczny wzór dla R_K, w którym wystarczy zamienić masy miejscami.

$\phi = -\frac {GM_Z \left (1 + \sqrt {\frac {M_K} {M_Z} } \right) } {d} -\frac {GM_K \left (1 + \sqrt {\frac {M_Z} {M_K} } \right)} {d}$

$\phi = -\frac {G} {d} \left (M_Z + \sqrt {M_ZM_K} + M_K + \sqrt {M_ZM_K} \right)$

$(7) \quad \phi = -\frac {G} {d} \left (\sqrt {M_Z} + \sqrt {M_K} \right)^2$

Taki wzór da również większą dokładność niż podstawienie odległości od obu ciał. Uzyskany wynik na potencjał grawitacyjny ze wzoru (7) wynosi około -1,28 ∙ 10⁶ [J/kg].

Zadanie 3

Jednym ze sposobów na rozwiązanie tego zadania byłoby zastosowanie rachunku całkowego, jednak tutaj zostanie przedstawiony nieco inny dowód, w którym nie będzie całek wprost.

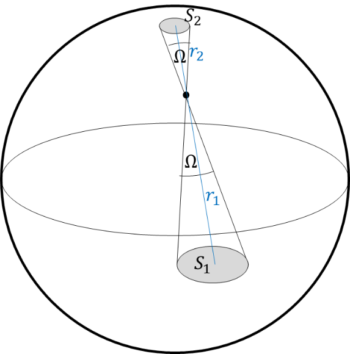
Radosław Kubiś

Wybierzmy dowolny punkt we wnętrzu sfery. Punkt ten będzie wierzchołkiem dla dwóch stożków, których podstawy leżą na powierzchni sfery. Oba stożki mają ten sam kąt bryłowy Ω. Kąt bryłowy jest definiowany jako stosunek powierzchni wycinka sfery, do kwadratu jej promienia (jak na rysunku):

$\Omega = \frac {S} {r^2}$

Należy jednak zauważyć, że w tym przypadku wierzchołek nie leży w środku sfery.Aby móc korzystać z definicji kąta bryłowego, trzeba przyjąć bardzo małe pola powierzchni (dużo mniejsze niż na rysunku), a co za tym idzie dużo mniejsze kąty bryłowe. Dla dostatecznie małych wartości zależność kąta od powierzchni będzie prawdziwa dla dowolnego punktu wewnątrz sfery.

$(1) \quad \Omega = \frac {S_1} {r_1^2} = \frac {S_2} {r_2^2}$

Teraz wprowadzimy pojęcie gęstości powierzchniowej. Jest to stosunek masy do powierzchni:

$(2) \quad \rho_S = \frac {m_1} {S_1} = \frac {m_2} {S_2}$

Wielkość ta będzie bardzo przydatna, bo jest stała dla naszej sfery, niezależnie od wielkości wyciętej powierzchni. Podstawmy jeszcze do równań na gęstość powierzchniową S₁ i S₂ z równań na kąt bryłowy.

$\rho_S = \frac {m_1} {\Omega r_1^2} = \frac {m_2} {\Omega r_2^2}$

$(3) \quad r_1^2 = \frac {m_1} {\Omega \rho_S},\quad r_2^2 = \frac {m_2} {\Omega \rho_S}$

Następnym krokiem będzie obliczenie natężenia pola grawitacyjnego pochodzącego od podstaw stożków w wybranym punkcie, czyli w przybliżeniu małych powierzchni wycinków sfery. Podobnie jak w zadaniu 2. natężenia od obu podstaw mają takie same kierunki, ale zwroty przeciwne, więc aby uzyskać wartość natężenia wypadkowego należy odjąć wartości składowych.

$(4) \quad \gamma = \frac {Gm_1} {r_1^2} - \frac {Gm_2} {r_2^2}$

Teraz za r₁² i r₂² można podstawić wielkości wyprowadzone w (3):

$\gamma = \frac {Gm_1 \Omega \rho_S} {m_1} - \frac {Gm_2 \Omega \rho_S} {m_2} = G \Omega \rho_S - G \Omega \rho_S = 0$

Jak widać, dla dwóch bardzo małych wycinków sfery natężenie się zeruje. Zauważmy jednak, że dla każdego niewielkiego wycinka istnieje taki, który zrównoważy jego oddziaływanie grawitacyjne
w punkcie wewnątrz sfery. Gdybyśmy teraz dodali wszystkie te malutkie wycinki uzyskalibyśmy całą sferę. Ponadto, punkt początkowy został wybrany dowolnie, a to oznacza, że dla każdego punktu wewnątrz sfery, natężenie pola grawitacyjnego będzie wynosić 0.

Źródła:

Tagi

Wydarzenia i imprezy

10. edycja European Rover Challenge zagości w Krakowie

Posted on 11 kwietnia 202411 kwietnia 2024 by Szymon Ryszkowski 641 odsłon

Setki młodych inżynierów rozpoczęło rywalizację o szansę uczestnictwa w finałach 10. jubileuszowej edycji European Rover Challenge (ERC). W tym roku 69 elitarnych drużyn, gotowych podjąć wyzwania naśladujące …

Zapisz się na obóz astronomiczny 2024

Posted on 30 marca 20247 kwietnia 2024 by Anna Wizerkaniuk 2k odsłon