Wśród zbioru oddziaływań słabych, grawitacja zdaje się nad wyraz wyróżniać. Oddziałuje na odległość, wpływa na wszystko i wszędzie, jest nawet w stanie zmieniać upływ czasu. Zjawiskiem, który łączy wszystkie jej wyjątkowości są oczywiście czarne dziury. Wyjątkowości jest jednak znacznie więcej niż można się spodziewać, a sięgają one nawet do cudownej kuchni słonecznej Italii.

Definicja słownikowa grawitacji prezentuje się następująco: „zjawisko naturalne polegające na tym, że wszystkie obiekty posiadające masę wzajemnie przyciągają się”. Jest to definicja szkolna i podstawowa, ale generalnie dopuszczająca. Stałe pozostają także skutki oddziaływań grawitacyjnych, które bezpośrednio mogą się jedynie różnić natężeniem. Definicję można jeszcze sformułować inaczej, z perspektywy domniemanego czwartego wymiaru. By taką definicję znaleźć, potrzebna jest podstawowa wiedza o czasoprzestrzeni, bo o kompletne zrozumienie tego pojęcia trudno.

Na początek trochę historii. W 1905, swoim annus mirabilis, urzędnik biura patentowego w Lucernie i absolwent ETH w Zurychu, niejaki Albert E., opublikował pięć prac. Najważniejszą, z punktu widzenia dzisiejszych czasów, zdaje się O elektrodynamice ciał w ruchu, gdzie zadebiutowała Szczególna Teoria Względności, łącząca maxwellowską elektrodynamikę oraz gaileuszowską zasadę względności. Teoria była oczywiście rozwijana, doczekała narodzin swojej młodszej, ale zdecydowanie bardziej majestatycznej siostry- Ogólnej Teorii Względności. Jednakże, to STW w 1907 roku stanowiła dla Hermana Minkowskiego podstawę do jej geometryzacji i w rezultacie wprowadzenia koncepcji czasoprzestrzeni.

W Internecie można znaleźć niezliczoną ilość sposobów na zrozumienie pojęcia przestrzeni Minkowskiego. Są czysto metaforyczne wizualizacje, w rodzaju bardzo dużej spandexowej płachty, rozciągniętej na okrągłym stelażu o parometrowym promieniu, na którą rzucona zostaje rzucona żelazna kula oraz mniejsza kauczukowa piłeczka, która to zaczyna krążyć wokół tej żelaznej (film 1). Mamy też czysto matematyczne przedstawienie sytuacji, w postaci skomplikowanych, często ciężkich w przyswojeniu wzorów. Oczywiście, początkujący najbardziej pomocnymi znajdą wizualizacje. Pozwalają one „zobaczyć” tak abstrakcyjne zjawisko jak zakrzywienie czasoprzestrzeni przez pryzmat codziennych doświadczeń. Ale abstrakcja, jeśli taką naprawdę jest, w całej swej okazałości może być podziwiana jedynie w czystej postaci. Jednakże, temat matematyki w tej przestrzeni jest zbyt obszerny, aby zawierać go w tym artykule, którego przecież nie jest meritum. Musimy tu wspomnieć mimo wszystko o pewnych filarach.

Film 1. Wizualizacja oddziaływania grawitacyjnego na czasoprzestrzeń za pomocą spandexu.

Dla ośrodkowych przestrzeni mamy w zasadzie tylko jedną istotną dla tematu przestrzeni Minkowskiego definicję: wartość wymiaru jest liczbą parametrów potrzebną do opisania danego punktu. Przestrzeń Minkowskiego nie ma wcale trudniejszej definicji. Jest to synteza czasu i przestrzeni 3-wymiarowej w czterowymiarową rozmaitość.

Podstawa teorii, przestrzeń 3-wymiarowa, jest prosta w zrozumieniu i dość dokładna. Wymiar czwarty może zostać zwizualizowany jako pewna ścieżka, równoległa do naszej przestrzeni, po której poruszamy się ze stałą prędkością, która jednak może zostać zniekształcona, a więc wydłużona, pod wpływem grawitacji. Taką ścieżką nazywa się czasoprostą. Interesujące jest, że to porównanie spełnia swoją rolę znakomicie również w przypadku tak zwanych osobliwości, gdzie materia jest niemal nieskończenie gęsta. Jeśli odejdziemy od metafory ścieżki, przechodząc do wyobrażenia czasoprzestrzeni, takie zniekształcenie przy osobliwości miałoby kształt zbliżony do tzw. trąbki Gabriela. Czas więc „wpłynąwszy” w taką osobliwość zatrzymuje się, z perspektywy obserwatora – staje.

Z czasoprostą wiąże się także pewne połączenie wymiaru trzeciego z czwartym. Jeśli spojrzymy na każdą trójwymiarową przestrzeń jako swoistą klatkę w filmie czasu, taka czasoprosta będzie tym, co te klatki spoi w jeden film. Będziemy więc mogli mówić o odległości między chwilami (klatkami): jedna sekunda będzie odpowiadała około 300 000 metrów.

Powyższe opisy to tylko czubek góry lodowej. Temat grawitacji jest bardziej niż tylko skomplikowany, a wyzwanie jej pojęcia i „połączenia” z innymi gałęziami fizyki podejmowane jest przez najtęższe umysły tego świata. Wszystkie te pojęcia zdają się jednak potrzebne, aby zbudować podstawy pod zrozumienie grawitacji pływowej z dwóch cudownie skorelowanych perspektyw.

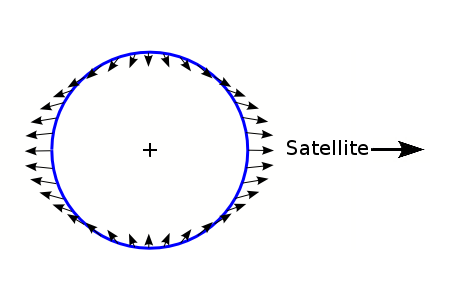
Najpierw przykład z życia. Będąc nad morzem, nie mamy możliwości by nie spotkać się z takim zjawiskiem jak przypływ, czy też odpływ. Panują wokół nich różne opinie: niektórzy są pewni, że odpływ występuje jedynie wieczorem, a przypływ rankiem, inni trwają w przekonaniu, że jest dokładnie odwrotnie. Obie te grupy się mylą! Pływy oceaniczne są skutkiem oddziaływania grawitacyjnego księżyca, a na skutek zjawiska grawitacji, właśnie- pływowej, tafla wody oceanicznej zostaje wybrzuszona nie tylko od strony naszego naturalnego satelity, ale i wprost odwrotnej (zdj. 2), co wyjaśnione zostanie w następnym akapicie. Dlatego kiedy przypływ obserwujemy w Sopocie, możemy się spodziewać, że jest on również obserwowany w okolicach australijskiego Melbourne. Ponadto z ruchów Księżyca wokół Ziemii wynika, że przypływy nie zajdą wyłącznie w nocy, ale zdarzy się także dzienny przypływ – zależy to od szerokości geograficznej, daty i godziny. 

Wikimedia Commons

(Zdj. 2.) Rozkład sił działających na ciało o krągłym przekroju pod wpływem grawitacji (naturalnego) satelity.

Aby zrozumieć mechanizm działania pływów, na początek zdefiniujmy samo pojęcie grawitacji pływowej. Nie ma czegoś takiego jak „rodzaj grawitacji” per se, grawitacja jest jedna zawsze. Ale! Ma różne skutki. Pływy są szczególnymi, gdyż można je rozumieć na wiele sposobów. Siły pływowe pojawiają się, gdy wielkość siły grawitacyjnej  zmienia się na długości ciała. Wynika to prosto ze wzoru , kiedy odległość między „początkiem” ciała a jego „końcem” jest na tyle znacząca, że różnica między przyspieszeniem grawitacyjnym  na części ciała bliższej źródłu grawitacji jest większa niż po drugiej stronie ciała. Grawitacja pływowa działa więc na nas zawsze, jednakże w naszej skali jest nieodczuwalna. Inaczej jest w przypadku bardziej masywnych ciał.

Oznaczmy siłę działającą na nogi astronauty krążącego wokół Ziemii przez , a przy głowie przez . Ze wzoru na przyspieszenie otrzymujemy więc  oraz , gdzie – wzrost astronauty, – odległość stóp astronauty od środka Ziemi. Stąd otrzymujemy wzór na różnicę przyspieszeń:

W tym przypadku z szeregu Taylora otrzymujemy następującą aproksymację , a więc . Ponadto, jak widać na schemacie poniżej (zdj. 3ab), z kształtu Ziemi i zmiennej odległości na przestrzeni ciała wynikają jeszcze dodatkowe siły, w układzie inercjalnym działające na skos na ręce, a w nieinercjalnym ściskające astronautę.

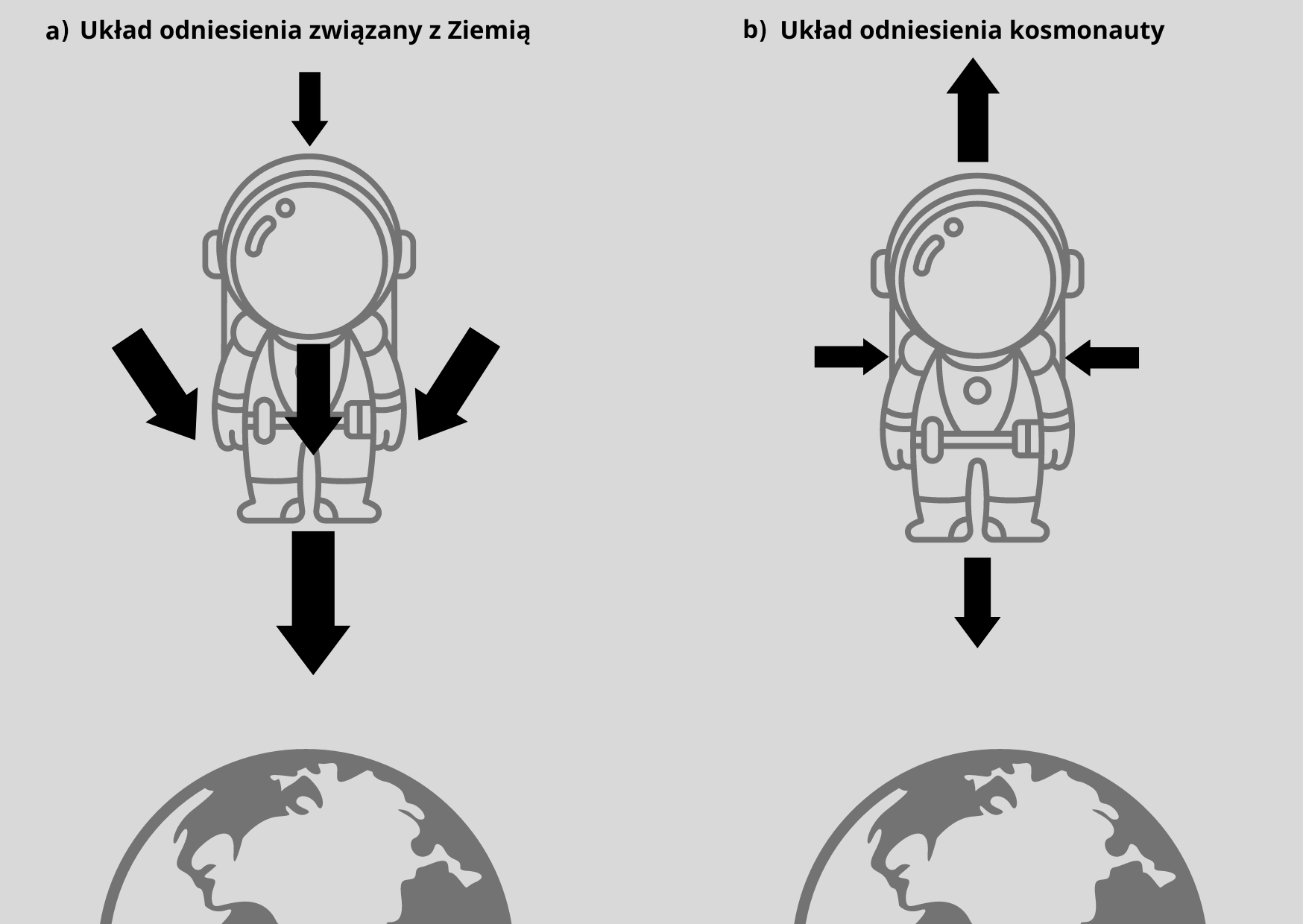
(Zdj. 3a i b) Rozkład sił grawitacyjnych w inercjalnym (a) i nieinercjalnym(b) układzie odniesienia.

Dla człowieka stojącego na Ziemi o wzroście 180 cm różnica przyśpieszenia wynosi , jest więc co najmniej nieodczuwalna. Na powierzchni Słońca wynosiłaby ona , byłaby więc mniejsza w przybliżeniu czterokrotnie. Niektórzy mogliby powiedzieć, że przecież Słońce ma większą masę, a więc  musi być większe. Mimo swojej masy, nie generuje tak znaczącego przyspieszenia na swojej powierzchni jak Ziemia, ze względu na znacząco mniejszą gęstość. Wynika to prosto ze przekształcenia wzoru Newtona przy użyciu zwykłej zależności gęstości i objętości. Wychodzi więc na to, że im większa gęstości obiektu, tym bardziej zauważalny jest efekt pływów. Przejdźmy więc do najgęstszych znanych nam obiektów – czarnych dziur.

Na potrzebę artykułu przyjmijmy definicję czarnej dziury jako obiektu, wokół którego rozpościera się horyzont zdarzeń, czyli teoretyczna granica, za którą oddziaływanie grawitacyjne jest na tyle silne, że nawet światło nie może jej przekroczyć – nie „wyleci” z czarnej dziury. Promień tej granicy, nazywany także promieniem Schwarzschilda, wyniesie  dla czarnej dziury o masie Słońca. Dla Sagittariusa A*, czarnej dziury w centrum Drogi Mlecznej, promień ten wyniesie . Z tego właśnie wyniknie nam różnica przyspieszeń. Podstawiwszy do wyprowadzonego wyżej wzoru na  wzór Schwarzschilda, dla czarnej dziury o masie Słońca otrzymujemy , ale już dla Sagittariusa A* wynik wyniesie zaledwie . Widać więc wpływ różnicy promieni na różnicę w obu przypadkach. Oznacza to także, że horyzont zdarzeń Sagittariusa A* moglibyśmy przekroczyć nawet tego nie zauważywszy. Niestety w przypadku Słońca, astronautę przekraczającego tą granicę czekałaby szybka śmierć. Szybka, ale szalenie interesująca w mechanizmie działania.

Wyobraźmy sobie astronautę orbitującego wokół gwiazdy neutronowej. Nazwijmy go Johnny. Pomijam tu takie aspekty jak temperatura, promieniowanie, bowiem to wszystko sprawiłoby, że Johnny zginąłby zanim jeszcze porządnie padłby ofiarą sił pływowych. W inercjalnym układzie odniesienia działają na niego przede wszystkim dwa wektory sił – w pobliżu stóp mocniejszy, w pobliżu głowy słabszy (zdj. 3a). Jednakże w układzie nieinercjalnym, cały obrazek sił zmienia się znacząco. Jak widać na zdjęciu 3b, wektor przy głowie zmieni swój zwrot o 180 stopni. Dojdą także dwa wektory „ściskające” Johnny’ego, wynikające z mechaniki materiału jakim jest ciało człowieka. Po chwili więc Johnny zostanie rozciągnięty wzdłuż i ściśnięty wszerz. Johnny już nigdy nie będzie już taki sam, Johnny będzie makaronem spaghetti. Stąd nazwa tego procesu – spaghettizacja.

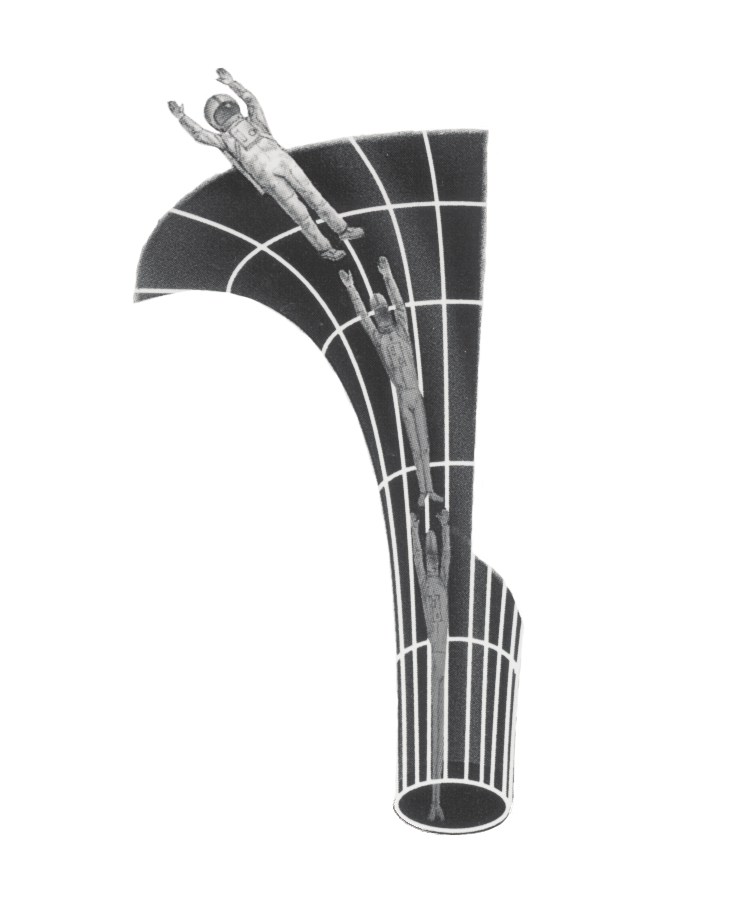
Można podjąć próbę zwizualizowania efektu makaronu na diagramie „w czterech wymiarach”, jak jest to pokazane na schemacie (zdj. 3.). W zrozumieniu tego pomoże fragment wiedzy z początku artykułu. Mamy tu bowiem do czynienia z analogiczną wizualizacją do spandexowej płachty albo też do procesu przepływania cieczy przez lejek. Ciecz dostosowuje się do jego geometrii – lej się zwęża, ciecz także. Analogicznie więc mamy lejek będący zakrzywieniem przestrzeni Minkowskiego, do którego astronauta musi się dostosować. Na tym przykładzie można także zrozumieć dlaczego mniejsze czarne dziury są o wiele bardziej niebezpiecznie względem tych masywniejszych. Cięższe istotnie bardziej zaginają czasoprzestrzeń, ale dzieje się to na większym obszarze. W przypadku lżejszych, to zakrzywienie jest mniejsze, lecz o większym nachyleniu.

Laura A. Whitlock, Kara C. Granger, Jane D. Mahon - The Anatomy of Black Holes An Information & Activity Booklet Grades 9-12, 1998-1999, Updated 2001

(Zdj. 4.) Schemat pomagający pojąć efekt dostosowania się do kształtu. Nie można go nazwać dokładnym ani całkowicie adekwatnym z oczywistego względu- miesza się tutaj wymiar trzeci z czwartym.

Wracając jednak do bardziej przyziemnych sytuacji, podobny efekt „dostosowania do kształtu” wpływa także na zachowanie niepołączonych obiektów wokół źródła grawitacji. To właśnie ona odpowiada za ich dostosowanie się do kształtu planety. Jako dobrze ilustrujący to zjawisko przykład może posłużyć układ czterech ciał w pobliżu źródła grawitacji. Jeśli na początku ułożone są one w kształt kwadratu tak, że jeden jego wierzchołek jest najbliżej źródła, a przekątna kwadratu wychodząca z tego punktu jest pod kątem prostym do stycznej do okręgu, o tym samym środku co okrąg źródła grawitacji, oddziałującej ten punkt, to po pewnym czasie, kształt ten ulegnie zmianie. Siły pływowe będą oddziaływać analogicznie do przykładu astronauty, będziemy więc mieli wówczas (jak na zdj. 5.) do czynienia z kształtem deltoidu.

Theresa Knott

(Zdj. 5.) Schemat działania sił na ciała zbliżające się do źródła grawitacji. Widoczna różnica pod względem kierunku między wektorami jest efektem działania siły grawitacyjnej zgodnie z kierunkiem prostopadłym do odpowiedniej stycznej względem źródła- możemy to tutaj nazwać spaghettifikacją.

Pomijając pływy, wszystko to jest teorią. Teoria Minkowskiego, jakkolwiek obiecująca, jest jedynie pomysłem na przyswojenie ledwo pojmowalnej natury związku czasu i grawitacji. Jeśli chodzi o spaghettizację, nie dysponujemy wystarczającymi środkami komunikacji interplanetarnej, aby potwierdzić możliwość zajścia takiego zjawiska, jednakże nie traćmy nadziei. Jeśli w przyszłości ta odległe podróże byłyby możliwe, możemy być pewni jednego – niespotykany dotąd rozwój zaszczyci włoską kuchnię.