Niniejszy artykuł przewidziany jest jako początek serii poruszającej podstawowe zagadnienia astronautyki, która nie stroniąc od technicznych szczegółów pozwoli czytelnikom na głębsze zrozumienie tematu. W ten sposób chciałbym zamknąć pewną lukę jaka istnieje pomiędzy artykułami popularnonaukowymi traktującymi najczęściej o najnowszych misjach kosmicznych, w których rzadko znajdziemy jakiekolwiek szczegóły, a literaturą naukową, która wymaga pewnej podstawowej wiedzy, aby w ogóle zacząć ją czytać. Oczywiście większość przedstawianej tutaj wiedzy jest dostępna w różnych źródłach, jednak rzadko kiedy jest ona skonsolidowana w sposób przydatny dla osób rozpoczynających swoją przygodę z astronautyką.
Rozpoczynamy tematem orbit, które są niejako centralnym pojęciem w astronautyce i jednym z pierwszych elementów planowania podczas przygotowań do jakiejkolwiek misji kosmicznej. Zacznijmy od krótkiego eksperymentu myślowego, który pozwoli nam zrozumieć dlaczego niektóre popularne poglądy w tym temacie są błędne. Wyobraźmy sobie, że stoimy na Ziemi i podskakujemy, czyli nadajemy naszemu ciału prędkość początkową. Oczywiście każdy z łatwością odpowie na pytanie co się wtedy stanie: za sprawą siły grawitacji stopniowo wytracimy naszą prędkość, osiągniemy jakąś wysokość maksymalną, a następnie zaczniemy przyspieszać w stronę Ziemi. W takim razie zmieńmy skalę tego zjawiska i zamiast typowej prędkości początkowej rzędu kilku metrów na sekundę wyobraźmy sobie, że jesteśmy w stanie nadać swojemu ciału prędkość na przykład 7 km/s (w tych rozważaniach pomińmy opór powietrza). Co się wówczas stanie? Większość z Czytelników odpowie zapewne, że to samo i mają oczywiście rację. Dopóki nasza prędkość początkowa nie osiągnie wartości około 12 km/s nie „wyrwiemy się” z wpływu grawitacyjnego Ziemi (o tym dlaczego tak jest dowiecie się w dalszej części artykułu), zatem przebieg naszego skoku będzie identyczny, jedynie zwiększy się wysokość jaką osiągniemy. W tym wypadku raczej nie poradzilibyśmy sobie bez skafandra kosmicznego — nasz skok wykroczyłby dość daleko poza granice atmosfery. Czy jednak osiągnęliśmy tym samym orbitę? Osoby zainteresowane astronomią i astronautyką jasno odpowiedzą, że nie, ponieważ po naszym skoku znów wróciliśmy na powierzchnię Ziemi. Osiągnęliśmy więc jedynie tzw. trajektorię sub-orbitalną, czyli swobodny tor ruchu pozwalający na znalezienie się na pewnej (znaczącej) wysokości nad Ziemią, ale rozpoczynający się i kończący na jej powierzchni. W tej definicji słowo ,,swobodny” oznacza, że podczas skoku nie działa na nas żadna siła poza siłą grawitacji, która, jak już zobaczyliśmy w naszym eksperymencie myślowym, jest dla nas szczególnie istotna. To ona i tylko ona będzie „rządziła” ruchem ciał rozważanych w tym artykule.
Widać więc, że sprawa osiągnięcia orbity nie jest taka prosta, nie wystarczy bowiem „podskoczyć” na odpowiednią wysokość. Spróbujmy więc innej strategii — podskoczmy pod pewnym kątem, tzn. sprawmy, że nasza prędkość początkowa nie będzie prostopadła do powierzchni ziemi. Dodatkowo założymy, że znajdujemy się na pewnym (bardzo spiczastym) wzniesieniu. Sytuację w skali małej, czyli gdy nasza prędkość wynosi tylko kilka metrów na sekundę przedstawia Rys. 1. Co bardziej dociekliwy Czytelnik wie zapewne, że w fizyce taką sytuację nazywamy rzutem ukośnym (tutaj zmodyfikowanym o obecność wzniesienia). Po rozwiązaniu równań ruchu można pokazać, że torem ruchu ciała będzie parabola.
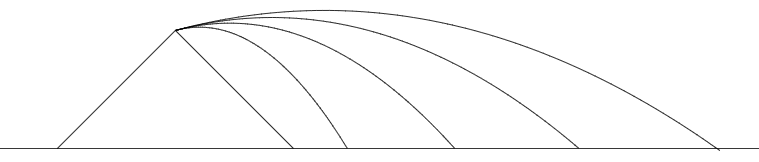
Rys. 1: Trajektorie skoku w małej skali przy różnych wartościach prędkości początkowej, ale tym samym kącie nachylenia jej wektora do powierzchni Ziemi.
Warto jednak pamiętać, że ten model dotyczy tylko i wyłącznie małej skali, z dwóch powodów:
- założona jest płaskość Ziemi, co w małej skali jest oczywiście rozsądne, natomiast w skali większej jej krzywizna zaczyna mieć znaczenie,
- używane jest równanie
tj. założyliśmy jednorodność pola grawitacyjnego.
Jak łatwo się domyślić, ten model nie pozwala wcale na zademonstrowanie osiągnięcia orbity, ponieważ oba te założenia w interesującym nas przypadku są błędne. Niemniej jednak, ze względu na intuicyjne zrozumienie tej sytuacji, możemy zaobserwować bardzo istotny fakt: w miarę zwiększania prędkości początkowej rośnie dystans jaki pokonujemy, a nasz tor ruchu się „wypłaszcza”. Przenieśmy teraz nasze doświadczenia na model bardziej rzeczywisty, który uwzględni krzywiznę Ziemi. Podobny eksperyment myślowy wykonał Newton, stąd zwykle nazywa się podobny przykład działem Newtona. Tym razem skakać (lub jak w oryginale wystrzeliwać pociski) będziemy dokładnie równolegle do powierzchni Ziemi. Widzimy to na Rys. 2.
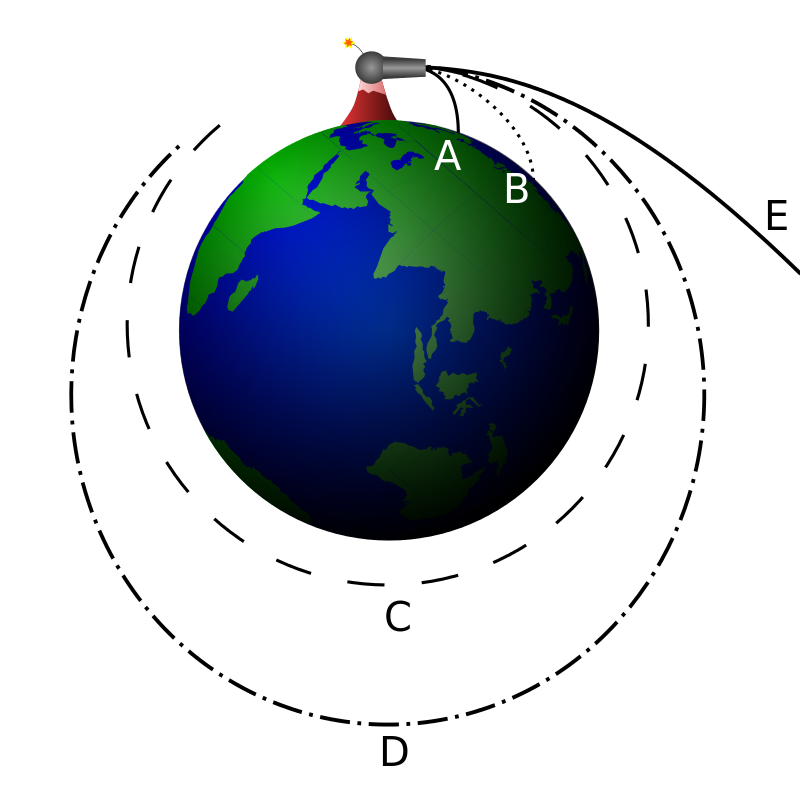 wikipedia.org
wikipedia.orgRys. 2: Zobrazowanie eksperymentu myślowego nazywanego działem Newtona.
Jak widać nasze skoki o małej prędkości wyglądają praktycznie identycznie jak te z poprzedniego przykładu, ale już krzywa oznaczona literą C ma zasięg nieskończony — po skoku nie dotykamy Ziemi tylko ją okrążamy, a zatem osiągamy orbitę. Czy więc oznacza to, że ”oszukaliśmy” grawitację — czyżby przestała na nas działać? Nie, po prostu poruszamy się tak szybko, że nasz tor ruchu ,,wypłaszczył” się bardzo znacząco i jego krzywizna jest dokładnie równa krzywiźnie Ziemi. Innymi słowy,cały czas spadamy na Ziemię, ale ze względu na naszą poziomą prędkość przez cały czas w nią nie trafiamy. Warto tu dodać, że ze względu na to, że poza uwzględnieniem krzywizny Ziemi w tym modelu używa się też bliższego rzeczywistości wzoru na siłę grawitacji () to tym razem krzywe po których porusza się ciało są elipsami, a nie parabolami (dla małych prędkości skoku różnica między tymi krzywymi jest bardzo nieznaczna).
Widzimy więc teraz, że prędkość jest kluczowym elementem dla osiągnięcia orbity. Dlatego też dość często mówi się o tak zwanej pierwszej prędkości kosmicznej, czyli prędkości teoretycznie najniższej możliwej orbity nad ciałem niebieskim. Jest to orbita kołowa na zerowej wysokości nad jego powierzchnią. Oczywiście, ze względu na przeszkody terenowe i obecność atmosfery,w przypadku Ziemi taka orbita nie jest możliwa do zrealizowania, natomiast w bardzo prosty sposób można tą prędkość znaleźć pamiętając, że dla orbity kołowej to właśnie grawitacja jest siłą powodującą zakrzywienie toru ruchu, czyli tzw. siłą dośrodkową. Miejmy świadomość, że jest to bardzo wyidealizowany przypadek — dla orbity kołowej siła grawitacji działa zawsze prostopadle do wektora prędkości powodując jedynie zmianę jego kierunku (czyli zakrzywienie toru), ale nie wartości. W tym właśnie przypadku można łatwo znaleźć wzór (1) na tę prędkość:
(1)
Znajdujemy w nim M, czyli masę ciała centralnego (np. Ziemi). Im większa jest ta masa tym większej prędkości potrzebujemy aby osiągnąć orbitę. Dalej znajdujemy R czyli promień ciała centralnego, który im większy tym niższa jest wymagana prędkość oraz G, czyli stałą grawitacji. Co może być zaskakujące, prędkość orbitalna nie zależy od masy ciała orbitującego. Gdy podstawimy do tego wzoru wartości odpowiadające Ziemi otrzymamy około 7,9 km/s, czyli właśnie pierwszą prędkość kosmiczną. Jednakże powyższa relacja prawdziwa jest dla dowolnej orbity kołowej jeżeli przyjmiemy, że R jest promieniem tej orbity. Widzimy więc, że prędkości liniowe są niższe na wyższych orbitach i tak na przykład na niskich orbitach okołoziemskich wynoszą nieco powyżej 7 km/s, a więc mniej niż pierwsza prędkość kosmiczna, ponieważ przebiegają na wysokościach powyżej atmosfery (najniższe używane orbity mają wysokość ok. 200 km nad powierzchnią Ziemi). Warto w tym miejscu dodać, że nasze rozważania uwzględniają jedynie wpływ ciała centralnego na ciało orbitujące pomijając wpływ odwrotny, zatem są prawdziwe tylko gdy masa ciała orbitującego jest znacznie mniejsza niż ciała centralnego. Dodatkowo pomijamy wpływ wszelkich innych ciał, które mogą znajdować się w pobliżu.
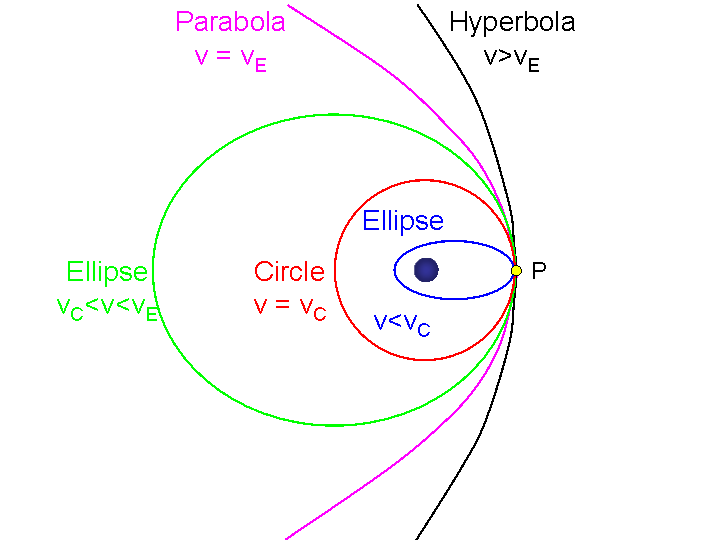
Krótko podsumujmy teraz co już wiemy. Osiągnięcie orbity możliwe jest tylko dzięki nadaniu ciału odpowiedniej prędkości i ta prędkość musi być odpowiednio skierowana — w przypadku orbity kołowej musi być ona nadana równolegle do powierzchni Ziemi, a jej wartość dobrana zgodnie z równaniem (1). Widzimy więc, że rakieta kosmiczna użyta do wyniesienia satelity na zadaną orbitę kołową ma 2 zadania — osiągnąć odpowiednią wysokość oraz prędkość (to oznacza właściwą wartość jak i kierunek). Oba te warunki muszą być spełnione, aby po separacji satelity pozostawał on na zadanej orbicie bez używania napędu. Dlatego też rakiety startują zwykle pionowo (aby uniknąć strat energii spowodowanych oporami aerodynamicznymi), ale już na pewnej wysokości zaczynają się pochylać, aby osiągnąć w końcu prędkość całkowicie poziomą (czyli równoległą do powierzchni Ziemi), tylko w ten sposób mogą na końcu swojej pracy spełnić warunki wymienione powyżej. W tej części artykułu to już koniec, w następnych zajmiemy się innymi przypadkami orbit — eliptycznymi, parabolicznymi i hiperbolicznymi.
Druga część cyklu dostępna tutaj.