Posted on   by 12k odsłon 

W dotychczas publikowanych w tej serii artykułów z mechaniki nieba szczegółowo omówione zostało rozwiązanie tzw. problemu dwóch ciał, czyli zagadnienia polegającego na znalezieniu trajektorii ruchu jednego ciała względem drugiego oraz dodatkowych zależności opisujących ten ruch, takich jak prawa Keplera.

Autorem artykułu jest Aleksander Łyczek

Problem trzech ciał

W praktyce bardzo często spotyka się układy złożone z więcej niż dwóch obiektów, jak chociażby nasz Układ Słoneczny i pozostałe układy planetarne co do których mamy pewność, że zawierają więcej niż jedną planetę, czy też układy wielokrotne gwiazd. Najlepszym przykładem jest leżący najbliżej Słońca układ gwiazd – α Centauri, złożony z dwóch gwiazd ciągu głównego (α Centauri A i B) o charakterystyce widmowej zbliżonej do naszej dziennej gwiazdy, oraz oddalonego od nich mniejszego towarzysza w postaci czerwonego karła, znanego powszechnie jako Proxima Centauri (α Centauri C).

Ze względu na znaczne oddalenie trzeciego składnika od dwóch głównych gwiazd – odległość Proximy od środka masy układu jest średnio około 1000 razy większa niż dystans między składnikami A i B – oraz jego prawie 10 razy mniejszą masę niż każda z pozostałych gwiazd, układ trzech ciał można de facto potraktować jako „podwójny układ podwójny”. Wpływ grawitacyjny składnika C na pozostałe dwa jest pomijalny w stosunku do siły ich wzajemnego oddziaływania, co pozwala w pierwszym, bardzo dobrym przybliżeniu, rozpatrywać osobno ruch składników A i B względem siebie oraz ruch Proximy wokół większych towarzyszy, zastępując ich pojedynczym obiektem o masie równej sumie mas tych gwiazd umieszczonym w środku masy układu.

W ogólnym jednak przypadku, w którym układ jest złożony z trzech lub więcej ciał, nie istnieje nawet przybliżone rozwiązanie analityczne układu równań różniczkowych opisujących ruch obiektów. Istnieje jedynie kilka szczególnych sytuacji w których trajektorie obiektów można opisać jawnym równaniem. Dotyczą one przede wszystkim układu trzech ciał, w którym najmniejszy obiekt jest dużo mniej masywny niż pozostałe dwa lub spełnione są pewne warunki odnośnie jego położenia. Bez wątpienia jednym z nich jest znaczne oddalenie trzeciego ciała od środka układu, jak to ma miejsce we wspomnianym już przypadku α Centauri, jednak analizując sytuację dokładniej, można znaleźć jeszcze parę punktów, w których jeżeli umieścimy małe ciało na początku ruchu, będzie można opisać jego trajektorię w sposób jawny.

Punkty Lagrange’a

Wspomniane na końcu wstępu punkty to tzw. punkty Lagrange’a, o których niektórzy Czytelnicy mogli już wcześniej słyszeć. Znane także jako punkty libracyjne, od łacińskiego słowa libra, oznaczającego wagę – wynika to z faktu, że w punktach tych następuje równowaga sił grawitacyjnych i bezwładności, dzięki czemu umieszczone w nich ciało nie zmienia swojego położenia względem pozostałych dwóch większych obiektów. Istnienie oraz zależności na położenie tych punktów zostały wyprowadzone po raz pierwszy w XVIII w. przez jednego z geniuszy epoki, francuskiego matematyka Josepha Lagrange’a. Przyjrzymy się teraz bliżej owemu wyprowadzeniu.

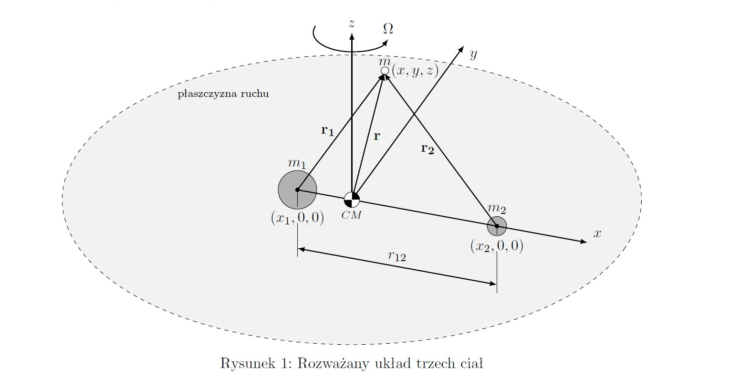
Załóżmy, że mamy dane dwa ciała o masach m_1 oraz m_2 okrążające środek masy po orbitach kołowych. Wprowadźmy układ współrzędnych o początku w środku masy układu i wraz z nim rotujący z prędkością kątową \omega, aby oś X cały czas pokrywała się z prostą łączącą składniki 1 i 2. Płaszczyzna XY pokrywa się z płaszczyzną orbity, oś Z stanowi oś obrotu układu. Jest to układ nieinercjalny, co powoduje konieczność uwzględnienia w późniejszych rozważaniach siły bezwładności, którą w przypadku układów rotujących ze stałą prędkością kątową stanowią siła odśrodkowa oraz siła Coriolisa.

Aleksander Łyczek

W tak zdefiniowanym układzie ciała m_1 i m_2 zlokalizowane są odpowiednio w punktach (x_1,0,0) oraz (x_2,0,0). Wprowadźmy trzecie ciało o masie m (m\ll m_1,m_2) w dowolnym punkcie o współrzędnych (x,y,z), którego początkowy wektor położenia wynosi \mathbf{r}=[x,y,z] względem środka masy układu (wektory będą dalej oznaczane poprzez pogrubienie tekstu) oraz \mathbf{r_1}=[x-x_1,y,z] oraz \mathbf{r_2}=[x-x_2,y,z] względem odpowiednich składników układu. Rozważaną sytuację przedstawiono na rysunku 1.

Naszym celem jest wyprowadzenie równań ruchu ciała o masie m, tzn. znalezienie zależności między położeniem \mathbf{r}, prędkością \mathbf{\dot{r}} i przyspieszeniem ciała \mathbf{\ddot{r}} w czasie. Gwoli informacji dla mniej zaawansowanych czytelników, kropka nad oznaczeniem funkcji (a wektor położenia jest de facto funkcją czasu) oznacza jej pochodną po czasie, czyli tempo jej zmian. Nietrudno zauważyć, że w takim razie prędkość jest niczym innym jak pierwszą pochodną położenia po czasie, zaś przyspieszenie jest pochodną prędkości, a tym samym drugą pochodną położenia po czasie, stąd dwie kropki w oznaczeniu.

Zacznijmy od wyznaczenia prędkości kątowej, z którą obiegają się składniki 1 i 2. Orbita tych składników jest kołowa, zatem można zastosować wzór na prędkość kątową w ruchu po okręgu:

(1)   \begin{equation*} \Omega=\frac{2\pi}{T} \end{equation*}

gdzie T oznacza okres wzajemnego obiegu głównych składników. Można go wyznaczyć, korzystając z III prawa Keplera:

(2)   \begin{equation*} T=2\pi\frac{r_{12}^{3\over 2}}{\sqrt{G(m_1+m_2)}} \end{equation*}

Zatem

(3)   \begin{equation*} \Omega = \sqrt{\frac{G(m_1+m_2)}{r_{12}^3}} \end{equation*}

Ciała m_1 i m_2 leżą na osi X, więc ich współrzędne y i z wynoszą 0. Współrzędne x można wyznaczyć, wykorzystując zależność na położenie środka ciężkości:

(4)   \begin{equation*} m_1 x_1+m_2 x_2 = (m_1+m_2)x_{CM}=0 \end{equation*}

Dodatkowo uwzględniając, że x_2-x_1=r_{12}, otrzymamy, że:

(5)   \begin{gather*} x_1=-\frac{m_2}{m_1+m_2}r_{12}=-\pi_2 r_{12} \\ x_2=\frac{m_1}{m_1+m_2}r_{12}=\pi_1 r_{12} \end{gather*}

Aby otrzymać równanie ruchu mniejszego ciała, skorzystamy z drugiej zasady dynamiki Newtona, która głosi, że przyspieszenie obiektu jest wprost proporcjonalne do siły wypadkowej nań działającej i odwrotnie proporcjonalne do masy tego ciała: \mathbf{\ddot{r}}=\frac{\mathbf{F}}{m}. Zastanowić się zatem należy, jakie siły, uwzględniając także siły bezwładności, działają na ciało m. Są to kolejno:

  • siły grawitacji od ciał m_1 i m_2 (minus wynika z faktu, że siły te są zwrócone przeciwnie do wektorów \mathbf{r_1} i \mathbf{r_2}):

    (6)   \begin{gather*} \mathbf{F_1}=-\frac{Gm_1 m}{r_1^3}\mathbf{r_1}\\ \mathbf{F_2}=-\frac{Gm_2 m}{r_2^3}\mathbf{r_2} \end{gather*}

  • siły bezwładności, odśrodkowa \mathbf{F_r} oraz Coriolisa \mathbf{F_c}:

    (7)   \begin{gather*} \mathbf{F_r}=-m\mathbf{\Omega}\times(\mathbf{\Omega}\times\mathbf{r})\\ \mathbf{F_c}=-2m\mathbf{\Omega}\times \mathbf{\dot{r}} \end{gather*}

Dla mniej zaawansowanych Czytelników, symbol ’\times’ oznacza tzw. iloczyn wektorowy, który dla wektorów trójelementowych \mathbf{v_1}=[a_1,b_1,c_1] i \mathbf{v_2}=[a_2,b_2,c_2] definuje się nastepująco:

    \begin{equation*} \mathbf{v_1} \times \mathbf{v_2}=[b_1c_2-c_1b_2,c_1a_2-a_1c_2,a_1b_2-b_1a_2] \end{equation*}

Ponieważ oś Z jest osią obrotu układu, wektor prędkości kątowej jest do niej równoległy, zatem \mathbf{\Omega}=[0,0,\Omega]. Podstawiając wszystkie wektory do równań od 6 do 7, otrzymamy:

(8)   \begin{equation*} \mathbf{F_1}=-\frac{Gm_1 m}{r_1^3}[x-x_1,y,z]=-\frac{Gm_1 m}{r_1^3}[x+\pi_2 r_{12},y,z] \end{equation*}

(9)   \begin{equation*} \mathbf{F_2}=-\frac{Gm_2 m}{r_2^3}[x-x_2,y,z]=-\frac{Gm_2 m}{r_2^3}[x-\pi_1 r_{12},y,z] \end{equation*}

(10)   \begin{equation*} \mathbf{F_r}=-m[0,0,\Omega]\times([0,0,\Omega]\times[x,y,z])=m[0,0,-\Omega]\times[-\Omega y,\Omega x,0]=m[\Omega^2 x,\Omega^2 y,0] \end{equation*}

(11)   \begin{equation*} \mathbf{F_c}=-2m[0,0,\Omega]\times [\dot{x},\dot{y},\dot{z}]=-2m[-\Omega \dot{y},\Omega \dot{x},0]=2m[\Omega \dot{y},-\Omega \dot{x},0] \end{equation*}

Równanie ruchu przyjmuje więc następującą postać:

(12)   \begin{multline*} \mathbf{\ddot{r}}=[\ddot{x},\ddot{y},\ddot{z}]=\frac{\mathbf{F_1+F_2+F_r+F_c}}{m}=-\frac{Gm_1}{r_1^3}[x+\pi_2 r_{12},y,z]-\frac{Gm_2}{r_2^3}[x-\pi_1 r_{12},y,z]\\+[\Omega^2 x,\Omega^2 y,0]+2[\Omega \dot{y},-\Omega \dot{x},0] \end{multline*}

Rozpisując równania dla każdej z trzech składowych otrzymamy:

(13)   \begin{gather*} \ddot{x}-2\Omega \dot{y}-\Omega^2 x=-\frac{Gm_1}{r_1^3}(x+\pi_2 r_{12})-\frac{Gm_2}{r_2^3}(x-\pi_1 r_{12})\\ \ddot{y}+2\Omega \dot{x}-\Omega^2 y=-\frac{Gm_1}{r_1^3}y-\frac{Gm_2}{r_2^3}y\\ \ddot{z}=-\frac{Gm_1}{r_1^3}z-\frac{Gm_2}{r_2^3}z \end{gather*}

Powyższy układ równań nie posiada ogólnego rozwiązania analitycznego, natomiast można go wykorzystać do znalezienia położenia punktów równowagi, w których prędkość i przyspieszenie ciała m są zerowe, a tym samym zdaje się ono być w spoczynku względem głównych składników układu. Ciało umieszczone w takim punkcie, pozostanie w nim. Wstawiając warunki brzegowe:

    \begin{equation*} \dot{x}=\dot{y}=\dot{z}=0, \ \ddot{x}=\ddot{y}=\ddot{z}=0 \end{equation*}

do równań 13, otrzymujemy

(14)   \begin{gather*} -\Omega^2 x=-\frac{Gm_1}{r_1^3}(x+\pi_2 r_{12})-\frac{Gm_2}{r_2^3}(x-\pi_1 r_{12})\\ -\Omega^2 y=-\frac{Gm_1}{r_1^3}y-\frac{Gm_2}{r_2^3}y\label{eq:lag_2}\\ 0=-\frac{Gm_1}{r_1^3}z-\frac{Gm_2}{r_2^3}z\label{eq:lag_3} \end{gather*}

Z ostatniego równania wynika, że:

(15)   \begin{equation*} \left(\frac{Gm_1}{r_1^3}+\frac{Gm_2}{r_2^3}\right)z=0 \end{equation*}

a ponieważ oba wyrażenia w nawiasie, a tym samym ich suma, są dodatnie, równanie jest spełnione wtedy i tylko wtedy gdy z=0. Oznacza to, że punkty równowagi leżą w płaszczyźnie ruchu głównych składników.

Do analizy równań 14 a) i b) przyda nam się dodatkowo spostrzeżenie, że \pi_1+\pi_2=1, czyli \pi_1=1-\pi_2. Korzystając z tej wiedzy oraz równania 3, zakładając także y\neq 0 równania 14 a) oraz b) przedstawiają się następująco:

(16)   \begin{gather*} -\frac{G(m_1+m_2)}{r_{12}^3}x=-\frac{Gm_1}{r_1^3}(x+\pi_2 r_{12})-\frac{Gm_2}{r_2^3}(x-(1-\pi_2)r_{12})\\ -\frac{G(m_1+m_2)}{r_{12}^3}y=-\frac{Gm_1}{r_1^3}y-\frac{Gm_2}{r_2^3}y \end{gather*}

Dokonując kilku przekształceń, otrzymujemy, że:

(17)   \begin{gather*} \frac{x}{r_{12}^3}=\frac{m_1}{m_1+m_2}\frac{x+\pi_2 r_{12}}{r_1^3}+\frac{m_2}{m_1+m_2}\frac{x+\pi_2r_{12}-r_{12}}{r_2^3}=\pi_1\frac{x+\pi_2 r_{12}}{r_1^3}+\pi_2\frac{x+\pi_2r_{12}-r_{12}}{r_2^3}\\ \frac{1}{r_{12}^3}=\frac{m_1}{m_1+m_2}\frac{1}{r_1^3}+\frac{m_2}{m_1+m_2}\frac{1}{r_2^3}=\frac{(1-\pi_2)}{r_1^3}+\frac{\pi_2}{r_2^3}\label{eq:lag_tri2} \end{gather*}

Wstawiając wyrażenie z prawej strony równania 17b) w miejsce \frac{1}{r_{12}^3} w równaniu 17a), dostajemy:

(18)   \begin{equation*} \frac{x(1-\pi_2)}{r_1^3}+\frac{\pi_2 x}{r_2^3}=\frac{(1-\pi_2)(x+\pi_2 r_{12})}{r_1^3}+\frac{\pi_2 x-\pi_2 r_{12}+\pi_2^2 r_{12}}{r_2^3} \end{equation*}

Grupując wyrażenia z tym samym mianownikiem, dostajemy:

(19)   \begin{equation*} \frac{\pi_2 r_{12}(1-\pi_2)}{r_2^3}=\frac{\pi_2 r_{12}(1-\pi_2)}{r_1^3} \end{equation*}

Ponieważ 0<\pi_2<1 oraz r_{12}>0, ostatnie równanie jest spełnione wtedy i tylko wtedy, gdy r_1=r_2. Wstawiając tę równość do równania 17b) dostaniemy ostatecznie, że \frac{1}{r_{12}^3}= \frac{1}{r_1^3}= \frac{1}{r_2^3}, a tym samym r_1=r_2=r_{12}. Oznacza to ni mniej, ni więcej, jak to, że wszystkie 3 ciała są położone w wierzchołkach trójkąta równobocznego. W płaszczyźnie orbity istnieją dwa takie punkty w których mozna umieścić ciało m, aby tworzyło ono z głównymi składnikami trójkąt równoboczny. Punkty te zwyczajowo nazywa się punktami Lagrange’a numer 4 oraz 5, a oznacza przez L_4 i L_5.

Powstaje natomiast pytanie, co z punktami 1, 2 oraz 3? Otóż do tej pory zakładaliśmy, że y\neq 0. W przypadku, gdy y=0, otrzymujemy, że wektory położenia ciała m względem głównych składników są równe \mathbf{r_1}=[x+\pi_2 r_{12},0,0] oraz \mathbf{r_2}=[x-\pi_1 r_{12},0,0]=[x-(1-\pi_2) r_{12},0,0]. Wynika z tego, iż r_1=|x+\pi_2 r_{12}| oraz r_2=|x+\pi_2 r_{12}-r_{12}|. W takim przypadku równanie 17a) przyjmie ostatecznie postać:

(20)   \begin{equation*} \frac{(1-\pi_2)(x+\pi_2 r_{12})}{|x+\pi_2 r_{12}|^3}+\frac{\pi_2(x+\pi_2 r_{12}-r_{12})}{|x+\pi_2 r_{12}-r_{12}|^3}-\frac{x}{r_{12}^3}=0 \end{equation*}

Powyższe równanie można uprościć poprzez ubezwymiarowienie zmiennej x, wprowadzając oznaczenie \xi=\frac{x}{r_{12}}. Jeżeli wyciągniemy r_{12} przed każdy nawias i wartość bezwzględną r_{12}, to lewa strona będzie wyglądać następująco:

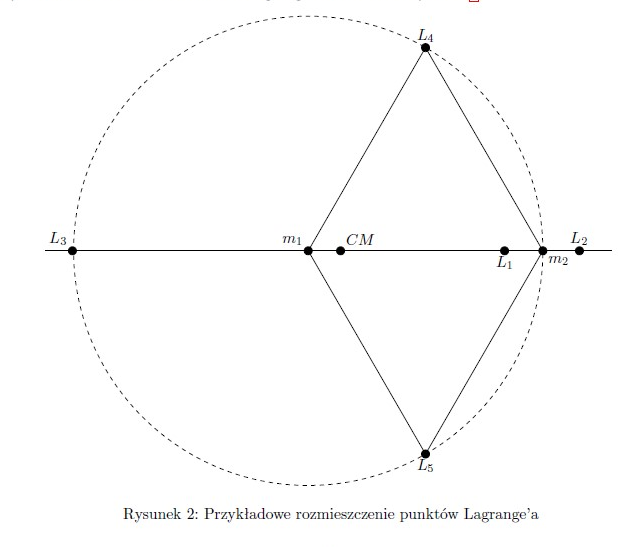
(21)   \begin{multline*} \frac{r_{12}(1-\pi_2)\left(\frac{x}{r_{12}}+\pi_2\right)}{r_{12}^3\left|\frac{x}{r_{12}}+\pi_2\right|^3}+\frac{r_{12}\pi_2\left(\frac{x}{r_{12}}+\pi_2-1\right)}{r_{12}^3\left|\frac{x}{r_{12}}+\pi_2-1\right|^3}-\frac{\frac{x}{r_{12}}}{r_{12}^2}=\\\frac{1}{r_{12}^2}\left(\frac{(1-\pi_2)(\xi+\pi_2)}{|\xi+\pi_2|^3}+\frac{\pi_2(\xi+\pi_2-1)}{|\xi+\pi_2-1|^3}-\xi\right)=\frac{1}{r_{12}^2}f(\xi) \end{multline*}

Zapis ten oznacza, że aby znaleźć brakujące punkty L_1, L_2 i L_3 wystarczy wyznaczyć miejsca zerowe funkcji f(\xi), co jest możliwe do zrobienia jedynie metodami numerycznymi. Punkty te leżą na prostej łączącej główne składniki, a oznaczenia odpowiadają następującym lokacjom:

  • L_1 – punkt leżący pomiędzy głównymi składnikami, -\pi_2<\xi_1<\pi_1
  • L_2 – punkt za mniejszym ciałem m_2, patrząc od strony większego składnika m_1, \xi_2>\pi_1
  • L_3 – punkt za większym ciałem m_1, patrząc od strony mniejszego składnika m_2, \xi_3<-\pi_2

Przykładowe rozmieszczenie punktów Lagrange’a przedstawia rysunek 2.

Aleksander Łyczek

Analizując zachowanie funkcji f(\xi) można pokazać, że posiada ona dokładnie 3 miejsca zerowe spełniające powyższe warunki, co teraz uczynimy. Rozważania te przydadzą nam się później w zadaniach.

Na wstępie należy zauważyć, że punkty \xi=-\pi_2 oraz \xi=\pi_1 nie należą do dziedziny funkcji. Dla pierwszego z nich mianownik członu \frac{(1-\pi_2)(\xi+\pi_2)}{|\xi+\pi_2|^3} przyjmuje wartość 0, zaś dla drugiego punktu to samo dzieje się z członem \frac{\pi_2(\xi+\pi_2-1)}{|\xi+\pi_2-1|^3} (pamiętamy, że \pi_1+\pi_2=1). To już nam powoduje, że musimy rozpatrywać tę funkcję na trzech przedziałach: -\infty<\xi<-\pi_2, -\pi_2<\xi<\pi_1 oraz \pi_1<\xi<\infty. Pokażemy, że f(\xi) jest monotoniczna w każdym z nich (na całej długości przedziału rośnie bądź maleje) oraz że wartości funkcji dla skrajnych punktów przedziałów leżą po przeciwnych stronach osi X. Oznacza to, że w danym przedziale funkcja przecina oś X w dokładnie jednym punkcie.

  1. -\infty<\xi<-\pi_2
    W tym przedziale \xi+\pi_2<0 oraz \xi+\pi_2-1<0, co implikuje równości

        \begin{gather*} |\xi+\pi_2|=-(\xi+\pi_2) \\ |\xi+\pi_2-1|=-(\xi+\pi_2-1) \end{gather*}

    Funkcja f(\xi) przyjmuje zatem postać

        \begin{equation*} f_1(\xi)=-\frac{1-\pi_2}{(\xi+\pi_2)^2}-\frac{\pi_2}{(\xi+\pi_2-1)^2}-\xi \end{equation*}

    Jeżeli \xi \rightarrow -\infty, to mianowniki obu ułamków jako kwadraty dążą do +\infty, czyli same wyrażenia zbliżają się do zera. Ostatni człon natomiast będzie zmierzał do -(-\infty), czyli +\infty, co równa się granicy całej funkcji w minus nieskończoności.Gdy \xi \rightarrow -\pi_2, to ostatnie dwa człony się kasują (-\pi_2-(-\pi_2), natomiast w pierwszym mianownik dąży do zera od dodatniej strony. Licznik także jest dodatni, zatem przez minus przed ułamkiem f_1(\xi)\xrightarrow[\xi \rightarrow -\pi_2]{}-\infty.
    Pokazaliśmy, że na krańcach przedziału funkcja dąży do przeciwnych nieskończoności, od dodatniej do ujemnej. Należy więc zatem udowodnić, że na całym przedziale jest ona malejąca, czyli dla dowolnych liczb rzeczywistych a, b, takich że -\infty<a<b<-\pi_2, f_1(a)>f_1(b). Nietrudno zauważyć, że jeżeli a<b, to -a>-b. Dodatkowo wyrażenia a+\pi_2, b+\pi_2, a+\pi_2-1, b+\pi_2-1 są wszystkie ujemne, co przy a<b implikuje nierówności (a+\pi_2)^2>(b+\pi_2)^2 oraz (a+\pi_2-1)^2>(b+\pi_2-1)^2, z których z kolei łatwo można dojść do postaci -\frac{1-\pi_2}{(a+\pi_2)^2}>-\frac{1-\pi_2}{(b+\pi_2)^2} oraz -\frac{\pi_2}{(a+\pi_2-1)^2}>-\frac{\pi_2}{(b+\pi_2-1)^2} poprzez odwrócenie oraz przemnożenie obu stron przez odpowiednie liczby ujemne, pamiętając o zmianie znaku nierówności przy każdej operacji. Ostatecznie otrzymujemy, że

        \begin{equation*} f_1(a)=-\frac{1-\pi_2}{(a+\pi_2)^2}-\frac{\pi_2}{(a+\pi_2-1)^2}-a>-\frac{1-\pi_2}{(b+\pi_2)^2}-\frac{\pi_2}{(b+\pi_2-1)^2}-b=f_1(b) \end{equation*}

    co dowodzi tego, ze funkcja f_1 jest malejąca na całym interesującym nas przedziale. W połączeniu z faktem o przeciwnych znakach wartości na krańcach przedziału wnioskujemy, że znajduje się w nim dokładnie jedno miejsce zerowe.

  2. -\pi_2<\xi<\pi_1
    W tym przedziale \xi+\pi_2>0 oraz \xi+\pi_2-1<\pi_1+\pi_2-1=0. Wynika z tego, iż:

        \begin{gather*} |\xi+\pi_2|=\xi+\pi_2 \\ |\xi+\pi_2-1|=-(\xi+\pi_2-1) \end{gather*}

    Funkcja f(\xi) będzie wyglądać więc następująco:

        \begin{equation*} f_2(\xi)=\frac{1-\pi_2}{(\xi+\pi_2)^2}-\frac{\pi_2}{(\xi+\pi_2-1)^2}-\xi \end{equation*}

    Tym razem dla \xi \rightarrow -\pi_2, f_2(\xi) dąży do +\infty, ponieważ mianownik pierwszego członu jest nieujemny, lecz tym razem nie ma znaku minus przed ułamkiem. Gdy \xi \rightarrow \pi_1, pierwszy i ostatni człon kasują się wzajemnie, zaś mianownik drugiego dąży do zera od dodatniej strony, lecz ze względu na minus przed ułamkiem, granicą funkcji w tym punkcie jest -\infty.Pozostaje pokazać, że funkcja w tym przedziale jest także malejąca na całej jego długości. Ponownie zakładamy a<b, co od razu daje nam nierówność -a>-b. \xi+\pi_2-1 jest znów ujemne na całym przedziale, co implikuje (a+\pi_2-1)^2>(b+\pi_2-1)^2, a tym samym -\frac{\pi_2}{(a+\pi_2-1)^2}>-\frac{\pi_2}{(b+\pi_2-1)^2}. \xi+\pi_2 jest tym razem dodatnie dla każdego \xi \in (-\pi_2,\pi_1), z czego wynika zależność (a+\pi_2)^2<(b+\pi_2)^2, a po odwróceniu obu stron \frac{1-\pi_2}{(a+\pi_2)^2}>\frac{1-\pi_2}{(b+\pi_2)^2}. Możemy zatem napisać, iż

        \begin{equation*} f_2(a)=\frac{1-\pi_2}{(a+\pi_2)^2}-\frac{\pi_2}{(a+\pi_2-1)^2}-a>\frac{1-\pi_2}{(b+\pi_2)^2}-\frac{\pi_2}{(b+\pi_2-1)^2}-b=f_2(b) \end{equation*}

    Ponownie udowodniliśmy, że funkcja jest malejąca jest malejąca na całej długości i na jego krańcach przyjmuje wartości o przeciwnych znakach, zatem posiada w nim dokładnie jedno miejsce zerowe.

  3. \pi_1<\xi<+\infty
    Dowód przebiega w zasadzie analogicznie jak w pozostałych dwóch przypadkach, tylko że tym razem zarówno \xi+\pi_2>0 oraz \xi+\pi_2-1>0, czyli zachodzą równości:

        \begin{gather*} |\xi+\pi_2|=\xi+\pi_2 \\ |\xi+\pi_2-1|=\xi+\pi_2-1 \end{gather*}

    Funkcja przybiera więc postać:

        \begin{equation*} f_3(\xi)=\frac{1-\pi_2}{(\xi+\pi_2)^2}+\frac{\pi_2}{(\xi+\pi_2-1)^2}-\xi \end{equation*}

    Znów wartość funkcji dąży do +\infty na lewym końcu przedziału ze względu na środkowy człon oraz do -\infty na skraju prawym z powodu ostatniego członu. Podobnie też dowodzimy, że funkcja jest malejąca na całym przedziale, czyli posiada w nim dokładnie jedno miejsce zerowe.

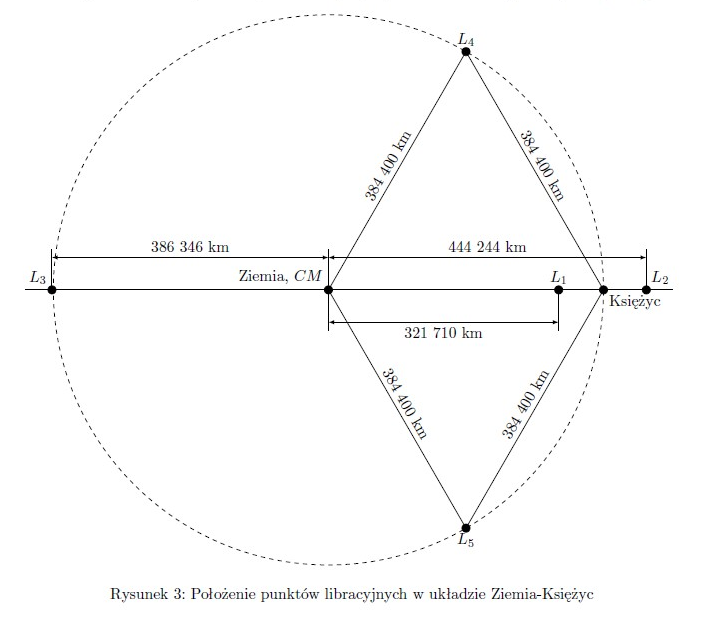
Zadanie

Wyznacz położenie punktów L_1, L_2 oraz L_3 w układzie Ziemia-Księżyc. Załóż, że orbita Księżyca wokół Ziemi jest okręgiem o promieniu R=384400 km, masa Ziemi wynosi M_Z=5{,}974\cdot 10^{24} kg, zaś masa Księżyca M_K=7{,}348\cdot10^{22} kg.

Wcześniej wspominaliśmy, że miejsca zerowe funkcji f(\xi) można wyznaczyć jedynie z wykorzystaniem metod numerycznych. Jednak istnieje jedna metoda, do której nie trzeba komputera, a wystarczy zwykły kalkulator naukowy. Metoda ta nazywa się metodą iteracji prostej i składa się z następujących kroków:

    1. Przekształcenie równania f(x)=0 do postaci x=g(x).
    2. Wybranie pierwszego przybliżenia rozwiązania równania x_0.
    3. Obliczenie x_1=g(x_0) jako kolejnego przybliżenia.
    4. Powtarzanie procedury uzyskiwania kolejnych przybliżeń x_{n+1}=g(x_n) do momentu aż różnica między kolejnymi wynikami |x_{n+1}-x_n| jest mniejsza niż ustalony przez nas próg błędu.

Oczywiście funkcja g(x) powinna także spełniać warunek |x_{n+1}-x_n|<|x_n-x_{n-1}|, aby uzyskać zbieżność rozwiązania. Z tego powodu poszukiwanie odpowiedniej g(x) może zająć trochę czasu i tak też jest w przypadku równań f_1(\xi)=0, f_2(\xi)=0 oraz f_3(\xi)=0. Narzucające się wręcz sprowadzenie tych równań do postaci:

    \begin{equation*} \xi=\pm \frac{1-\pi_2}{(\xi+\pi_2)^2} \pm \frac{\pi_2}{(\xi+\pi_2-1)^2} \end{equation*}

nie zdaje egzaminu dla żadnej z trzech rozważanych funkcji, algorytm rozwiązywania jest rozbieżny dla takiego przekształcenia. Po odpowiednio długich poszukiwaniach udało się znaleźć funkcje g_1(\xi), g_2(\xi) oraz g_3(\xi) (odpowiadające funkcjom f o tym samym indeksie), dla których procesy iteracji są zbieżne. Równania, które chcemy rozwiązać, mają kolejno postać:

    \begin{gather*} \xi=g_1(\xi)=-\sqrt{\frac{1-\pi_2}{-\xi-\frac{\pi_2}{(\xi+\pi_2-1)^2}}}-\pi_2 \\ \xi=g_2(\xi)=\frac{1}{1+\sqrt{\frac{\xi(\xi+\pi_2-1)^2+\pi_2}{1-\pi_2}}}-\pi_2\\ \xi=g_3(\xi)=\sqrt{\frac{1-\pi_2}{\xi}\left(1-\frac{1}{\xi+\pi_2}\right)^2+\frac{\pi_2}{\xi}}-\pi_2+1 \end{gather*}

Zanim przystąpimy do obliczeń, trzeba jeszcze wyznaczyć wartość \pi_2:

    \begin{equation*} \pi_2=\frac{M_K}{M_Z+M_K}=\frac{7{,}348\cdot10^{22}}{5{,}974\cdot 10^{24}+7{,}348\cdot10^{22}}=0{,}012151 \end{equation*}

Rozwiązania uzyskiwane w kolejnych iteracjach przedstawiono w tabeli ??. Przy wybieraniu wartości startowej należy pamiętać, by należała ona do przedziału, w którym każda z funkcji jest zdefiniowana, tzn. -\infty<\xi<-\pi_2 dla h_1(\xi), -\pi_2<\xi<\pi_1 dla h_2(\xi) oraz \pi_1<\xi<+\infty dla h_3(\xi).

\xih_1(\xi) (\xi_{L_3})h_2(\xi) (\xi_{L_1})h_3(\xi) (\xi_{L_2})
\xi_0-0,50,51,5
\xi_1-1,4255250,7207911,277064
\xi_2-0,845210,7855191,207947
\xi_3-1,0955640,8130791,179347
\xi_4-0,9629350,8257241,166565
\xi_5-1,0266880,8316431,160714
\xi_6-0,9944870,8344291,158014
\xi_7-1,0103610,8357431,156763
\xi_8-1,002440,8363621,156184
\xi_9-1,0063690,8366541,155915
\xi_{10}-1,0044140,8367921,15579
\xi_{11}-1,0053850,8368571,155732
\xi_{12}-1,0049020,8368881,155705
\xi_{13}-1,0051420,8369031,155693
\xi_{14}-1,0050230,8369091,155687
\xi_{15}-1,0050820,8369131,155684
\xi_{16}-1,0050530,8369141,155683
\xi_{17}-1,0050670,8369151,155682
\xi_{18}-1,005060,8369151,155682
\xi_{19}-1,005064
\xi_{20}-1,005062
\xi_{21}-1,005063
\xi_{22}-1,005062
\xi_{23}-1,005063
\xi_{24}-1,005063

Punkty Lagrange’a L_1, L_2 oraz L_3 układu Ziemia-Księżyc znajdują się zatem w następujących odległościach od środka masy składników:

    \begin{gather*} x_{L_1}=0{,}836915\cdot 384400 \ \rm km=321710 \ km \\ x_{L_2}=1{,}155682\cdot 384400 \ \rm km=444244 \ km \\ x_{L_3}=-1{,}005063\cdot 384400 \ \rm km=-386346 \ km \end{gather*}

Rozmieszczenie punktów libracyjnych zostało przedstawione na rysunku ??. Ze względu na położenie środka masy układu wewnątrz Ziemi, oba obiekty są reprezentowane na rysunku przez jeden punkt.

Aleksander Łyczek

Podsumowanie

W powyższych rozważaniach udowodniliśmy teoretycznie istnienie punktów równowagi w układach dwóch ciał, w których można umieścić trzecie, dużo mniejsze ciało, aby nie zmieniało ono swego położenia względem głównych składników. Oczywiście istnienie punktów Lagrange’a zostało potwierdzone także empirycznie. Najlepszym przykładem na to są tzw. planetoidy trojańskie, czyli małe obiekty Układu Słonecznego ,,schwytane” w punktach L_4 oraz L_5 układu Słońce-Jowisz. W sumie w obu punktach znajduje się przeszło 10000 planetoid, spośród których największa ma rozmiar 370\times200 km. Ich zgrupowanie w punktach L_4 oraz L_5 wynika z faktu, że te punkty jako jedyne spośród wszystkich pięciu zapewniają równowagę stabilną, tzn. po wychyleniu obiektu w nich umieszczonego będzie chciał on powrócić w uprzednio zajmowane miejsce.

Godne wspomnienia są także punkty L_1 oraz L_2 układu Słońce-Ziemia. Ze względu na bliskość Ziemi oraz właśnie niestabilną równowagę, która sprawia, że nie zalegają w nich pył oraz inne ,,kosmiczne śmieci”, są świetnym miejscem do umieszczania w nich naukowych misji kosmicznych. Punkt L_1 stanowi idealną lokację dla sond zajmujących się obserwacją Słońca, zaś punkt L_2 dla tych badających głęboki kosmos.

Tagi

Autor

Avatar photo
Redakcja AstroNETu

Podobne artykuły

Katalog Caldwella: C74

Posted on  

Jak przygotować się do Olimpiady Astronomicznej?

Posted on  

Start Olimpijskiej Ligi Astronomicznej

Posted on  

Uczestnicy IOAA 2023
16. Międzynarodowa Olimpiada z Astronomii i Astrofizyki

Posted on