Zdjęcie w tle: NASA
Część trzecia artykułu traktującego o orbitach z punktu widzenia astronautyki. Tym razem omówimy przypadki orbit parabolicznych i hiperbolicznych. Poprzednie części dostępne tutaj: część 1. i część 2.
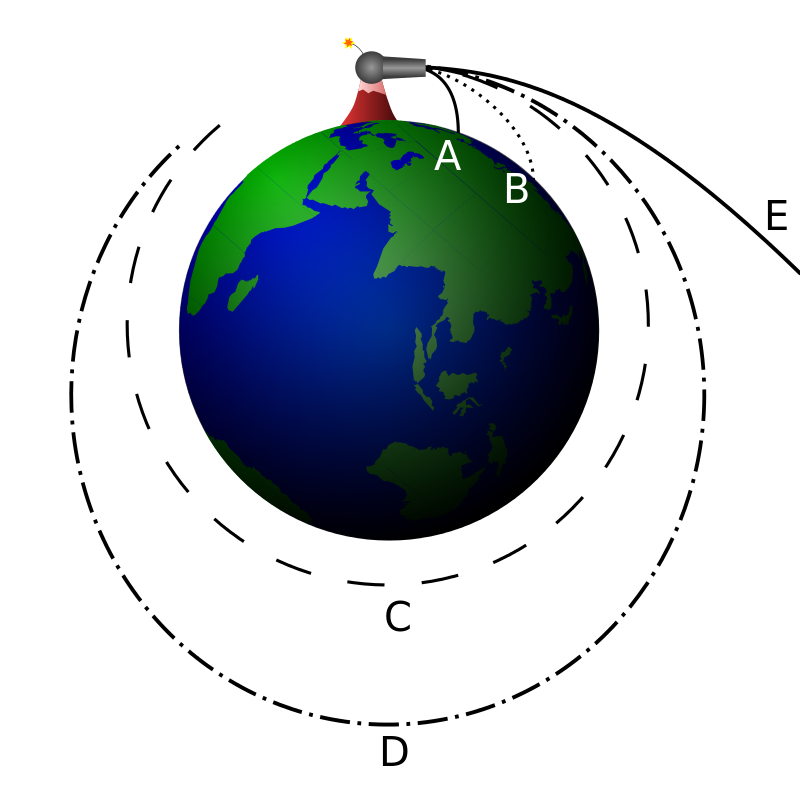
Nasza podróż poprzez różne typy orbit powoli dobiega końca, niemniej jednak wciąż pozostaje jedno zagadnienie, które do tej pory zręcznie omijaliśmy. Zakładaliśmy bowiem, że prędkości przez nas osiągane są na tyle małe, że nie pozwalają na „wyrwanie” się z pola grawitacyjnego Ziemi. To założenie jest oczywiście poprawne dla wszystkich ziemskich satelitów i ich orbity rzeczywiście są elipsami lub (w szczególnych przypadkach) okręgami. Jednakże, aby myśleć o misji międzyplanetarnej, musimy oczywiście wykroczyć poza to założenie. Patrząc na rysunek 1 znany z poprzednich części zastanówmy się więc co się stanie gdy stopniowo będziemy zwiększać prędkość naszego skoku. Już wiemy, że najpierw uda nam się zatoczyć orbitę kołową, następnie zaczniemy zataczać elipsy o coraz wyższym apocentrum (apogeum). Zwiększamy bowiem coraz bardziej swoją całkowitą energię mechaniczną, która na orbicie jest stała. Domyślamy się więc, że w pewnym momencie osiągniemy energię tak wysoką, że Ziemia nie będzie nas w stanie utrzymać w swoim polu grawitacyjnym. Tę sytuację przedstawia krzywa E na rysunku 1. Widzimy, że jest to krzywa otwarta. Można udowodnić, że pierwsza taka krzywa (dla minimalnej prędkości skoku pozwalającej na ucieczkę) jest fragmentem paraboli. Poniekąd wróciliśmy do początku, ale tym razem ta parabola jest zupełnie czym innym niż ta, którą rozważaliśmy dla małych prędkości skoku, zupełnie inne są bowiem poczynione założenia. Warto zauważyć, że w tym wypadku będziemy się oddalać w nieskończoność od Ziemi, przez co jej przyciąganie będzie stale słabnąć, ale nigdy nie będzie wynosić 0. Skutkuje to bardzo szczególną sytuacją, w której po nieskończonym czasie nasza prędkość zmalałaby do zera.
 Wikipedia
WikipediaRys. 1. Zobrazowanie eksperymentu myślowego nazywanego działem Newtona.
Ponieważ prędkość ucieczki jest bardzo charakterystyczną prędkością, otrzymała ona nazwę drugiej prędkości kosmicznej. Można ją obliczyć używając wyrażeń na energię potencjalną i kinetyczną ciała. Wiemy bowiem, że energia tego ciała musi wynosić zero nieskończenie daleko od Ziemi (energia potencjalna jest tam równa zero według definicji, a energia kinetyczna ze względu na zerową prędkość). Wiemy też, ile wynosi energia potencjalna na powierzchni Ziemi. Stąd możemy obliczyć, że druga prędkość kosmiczna wyniesie:
Podobnie jak w przypadku pierwszej prędkości kosmicznej, zauważamy zależność od masy M ciała centralnego, jego promienia R oraz stałej grawitacji G. Dla Ziemi, po podstawieniu wartości, dostaniemy 11,19 km/s. Warto zauważyć, że niezależnie jak zorientowany będzie wektor prędkości początkowej, ciało oddali się do nieskończoności. Przy wyprowadzeniu nie używaliśmy bowiem w ogóle pojęcia wektora, jedynie wartość prędkości była istotna. W każdym przypadku torem ruchu będzie fragment paraboli (lub, w szczególnym przypadku gdy wektor skierowany będzie dokładnie prostopadle do powierzchni, prostą). Jeszcze jedną prostą obserwacją jest fakt, że druga prędkość kosmiczna jest zawsze większa od pierwszej o czynnik . Wynika to po prostu z porównania wzorów na obie te prędkości.
Pozostaje więc pytanie, co jeżeli zwiększymy naszą prędkość początkową ponad drugą prędkość kosmiczną. Odpowiedzi większość czytelników może się domyślić. Nasza całkowita energia będzie teraz większa od zera, dlatego w nieskończonej odległości od Ziemi (po nieskończonym czasie) wciąż będziemy mieli jakąś niezerową prędkość. Co do toru ruchu to oczywiście musi się on jeszcze bardziej „wypłaszczyć” względem paraboli i tym razem będzie hiperbolą.
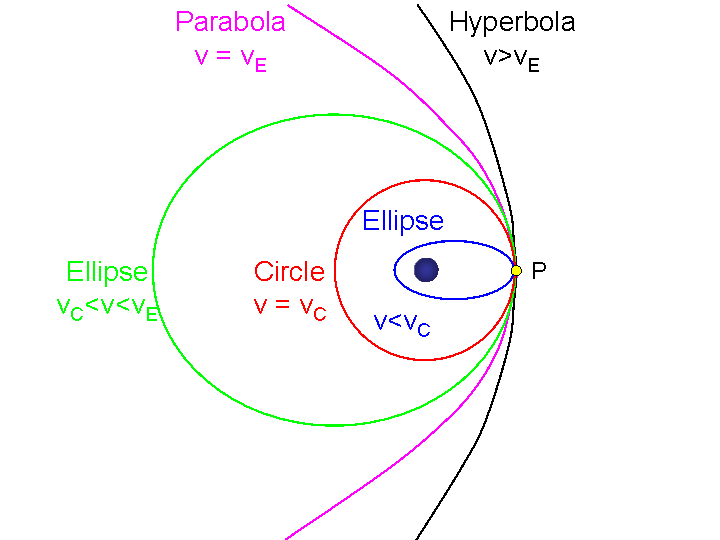
Jako podsumowanie artykułu zastanówmy się jakie orbity mogą być osiągnięte, nadając początkową prędkość równoległą do powierzchni Ziemi ciału znajdującemu się na pewnej znacznej wysokości. Sytuację tą przedstawia rysunek 2. Jeżeli nasza prędkość będzie niższa niż prędkość na odpowiadającej tej wysokości orbicie kołowej (vC) to nie mogąc poruszać się po okręgu, ciało zacznie zbliżać się do Ziemi, zataczając wokół niej elipsę i następnie wracając do punktu początkowego. Przy prędkości vC osiągnięta zostanie orbita kołowa, a dla wyższych elipsy o coraz wyższym apogeum. W końcu, gdy nadamy ciału prędkość ucieczki (vE) odpowiednią dla tej wysokości, zacznie się ono poruszać po paraboli i nigdy nie wróci do punktu początkowego. Dla prędkości wyższych niż vE ciało zacznie poruszać się po hiperboli i tak samo nigdy nie wróci do punktu początkowego.
 astronomy.ohio-state.edu
astronomy.ohio-state.eduRys. 2. Ilustracja różnych orbit możliwych do osiągnięcia poprzez nadanie prędkości początkowej w danym punkcie nad Ziemią.
To już koniec tego artykułu, który miał zaznajomić czytelników z tematyką orbit od zupełnych podstaw. Mam nadzieję, że po jego przeczytaniu prostsze będzie zrozumienie kolejnych artykułów z serii o astronautyce. Już w następnym zajmiemy się manewrami orbitalnymi, czyli co zrobić, by zmodyfikować parametry orbity w żądany sposób, co da nam podstawy zrozumienia, jak satelity umieszczane są na orbitach i jak przeprowadzane są misje międzyplanetarne.


