Tłumacząc prawa Keplera, możemy podejść do zagadnienia na dwa sposoby: idąc tropem uczenia Tychona de Brahe lub zgodnie ze współczesnym ujęciem. W tym artykule z drobnymi odstępstwami przedstawione zostanie drugie, współczesne podejście.

Artykuł napisał Szymon Antkowiak

Krzywe Stożkowe

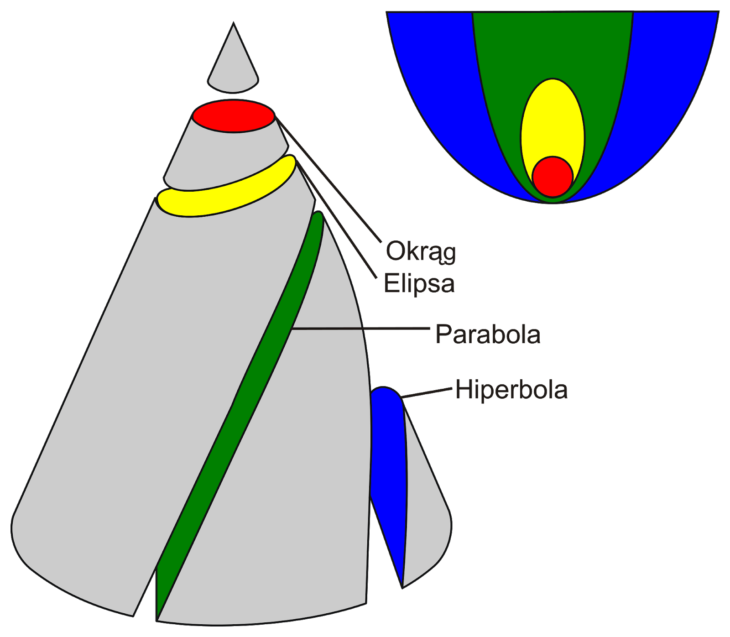
By dobrze zrozumieć prawa Keplera, potrzebna jest znajomość geometrii, która się w nich pojawia. W polu grawitacyjnym ciała o stałej energii poruszają się po krzywych stożkowych. Są to krzywe będące przecięciem powierzchni stożkowej przez płaszczyznę pod odpowiednim kątem. Należą do nich okręgi, elipsy, parabole i hiperbole. Dwie pierwsze to krzywe zamknięte, a dwie kolejne otwarte.

 

 

Wszystkie te krzywe wiąże mimośród, czyli stosunek odległości między ogniskiem a środkiem elipsy i długością osi wielkiej. Ogniska to punkty charakterystyczne tych krzywych (elipsa zdefiniowana jest jako zbiór punktów, których suma odległości od obu ognisk elipsy jest stała i równa 2a – dwóm półosiom wielkim). Na podstawie elipsy omówimy najważniejsze długości w krzywej stożkowej:

 

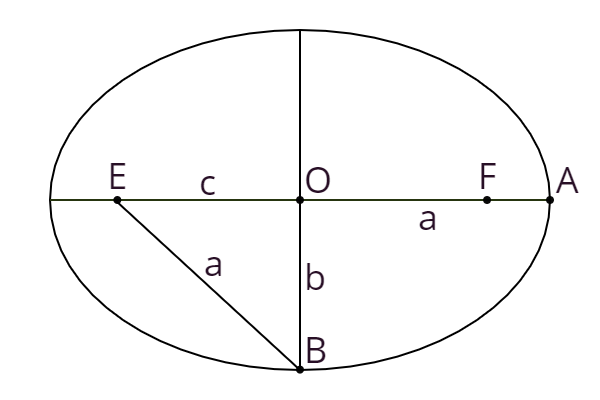
• Półoś wielka – odcinek OA, długość a, połowa najdłuższej średnicy elipsy (osi wielkiej), zawsze współliniowa z ogniskami.
• Półoś mała – odcinek OB, długość b, połowa najkrótszej średnicy elipsy (osi małej), zawsze prostopadła do osi wielkiej.
• Ogniska – punkty E i F, każdą krzywą stożkową można opisać z wykorzystaniem odległości od ognisk.
• Odległość ogniska od środka elipsy – odcinek OE i OF, długość c (w elipsie związany z półosiami wzorem )
• Mimośród – inaczej ekscentryczność, parametr opisujący krzywe stożkowe, będący stosunkiem odległości ogniska od środka do półosi wielkiej

Wiedząc, czym jest mimośród, możemy przyporządkować poszczególnym krzywym zakres wartości mimośrodu:

• Jeśli e=0 krzywa jest okręgiem – specjalnym przypadkiem elipsy, w której a=b.
• Jeśli 0<=e<1 krzywa jest elipsą. Im większe e tym elipsa jest bardziej spłaszczona.
• Jeśli e=1 krzywa jest parabolą.
• Jeśli e>1 krzywa jest hiperbolą.

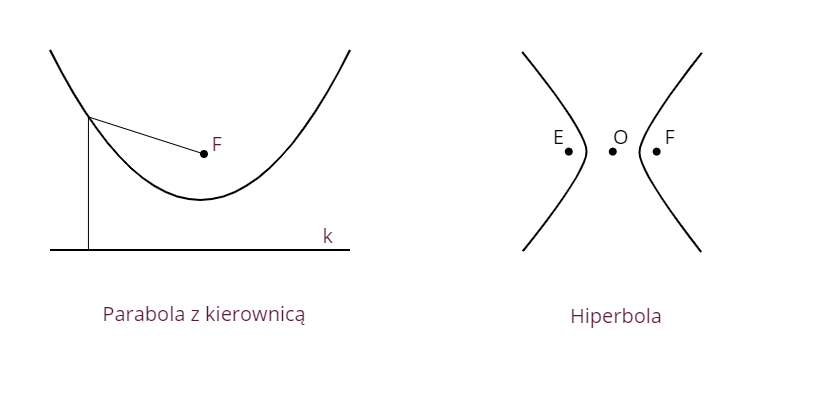
Parabola jest zbiorem punktów równoodległych od ogniska (punkt F na rysunku) i prostej zwaną kierownicą (prosta k na rysunku). Jako że paraboli odpowiada tylko jedna wartość mimośrodu (e=1) to każda parabola jest taka sama. Hiperbola natomiast jest zbiorem punktów, dla których wartość bezwzględna różnicy odległości od obu ognisk (punkty E i F) jest stała i równa 2a.

 

Inne przydatne wzory opisujące elipsę:

• Pole elipsy:
• odległość skrajnych punktów orbity od ogniska:
• zależność między półosiami:

I prawo Keplera

W układzie odniesienia związanym ze środkiem masy dwóch ciał niebieskich tor ich ruchu jest krzywą stożkową. Inaczej mówiąc, dwa niezależne od innych ciała poruszają się wokół wspólnego środka masy po krzywych stożkowych. Warto tutaj zaznaczyć, że obie krzywe mają taki sam mimośród, ale mogą różnić się rozmiarem.

Zależność geometryczna wiążąca krzywe to jednokładność o skali względem punktu środka masy. Jednokładność, o skali k względem O, to przekształcenie przyporządkowujące punktowi A punkt A’ taki, że 

II prawo Keplera

Jeżeli ciało ma stałą masę, to jego prędkość polowa na orbicie też jest stała. Własność ta wynika z zasady zachowania momentu pędu. Inaczej mówiąc iloraz pola zakreślonego przez odcinek łączący ognisko orbity z ciałem w czasie i czasu jest stały.

III prawo Keplera

Jeśli pominie się oddziaływania z ciałami spoza układu, to obowiązuje zależność , gdzie: a – to półoś wielka, po których poruszają się ciała wokół centrum masy, T – okres obiegu, G – stała grawitacji, m – masa. Dla Układu Słonecznego masa planet względem masy Słońca jest pomijalna, wówczas prawą stronę równości możemy uznać za stałą, otrzymując zaobserwowaną przez Keplera zależność .

Przykładowe zadania

1. Słońce obiega środek Drogi Mlecznej odległy od niego o  m w czasie lat. Załóżmy, że Słońce znajduje się na skraju galaktyki, średnia masa gwiazd jest równa masie Słońca oraz gwiazdy są równomiernie rozłożone w kuli o środku w centrum Drogi Mlecznej. Ile według takich założeń jest gwiazd w naszej galaktyce? Czy warunek równomiernego rozmieszczenia jest konieczny?
2. Wskutek wiatru słonecznego Słońce traci w ciągu roku kg swojej masy. Oblicz, jak ten ubytek masy wpływa na długość jednostki astronomicznej w czasie t = 1000 lat. Przyjmij, że orbita Ziemi jest okręgiem, a wiatr słoneczny nie wpływa bezpośrednio na ruch Ziemi.
3. Sztucznego satelitę Ziemi obserwowano w apogeum jego orbity. Wyznaczona odległość satelity od środka Ziemi wynosiła wtedy kilometrów, a geocentryczna prędkość kątowa satelity wynosiła radianów na sekundę. Zakładamy również znajomość masy Ziemi . Wyprowadź wzór pozwalający z tych danych obliczyć, po jakim czasie od momentu dokonanych pomiarów należałoby obserwować satelitę, aby prześledzić jego ruch w pobliżu perygeum.
4. Rozpatrujemy keplerowską orbitę gwiazdy podwójnej w układzie związanym z jednym z jej składników, nazywamy go gwiazdą centralną. Oblicz mimośród e tej orbity oraz kąt nachylenia i płaszczyzny orbity do płaszczyzny prostopadłej do kierunku widzenia, gdy obserwowana orbita, tj. rzut orbity na płaszczyznę prostopadłą do kierunku patrzenia, jest:
   1. elipsą o wielkiej półosi a = 1,6” i małej półosi b = 1,1”, a gwiazda centralna leży w środku tej elipsy, tzn. w punkcie przecięcia osi,
   2. okręgiem, a gwiazda centralna leży w połowie promienia tego okręgu,
   3. elipsą o wielkiej półosi a = 2,1” i małej półosi b = 1,4”, a gwiazda centralna leży dokładnie w połowie małej półosi tej elipsy.

Wskazówka: choć gwiazdy są w układzie podwójnym to z powodu wyboru gwiazdy centralnej i związania z nią układu odniesienia, całość można interpretować jako ruch jednego ciała wokół drugiego

Rozwiązania

Zadanie 1

Znając średnią masę gwiazdy w galaktyce, możemy oszacować ich liczbę, dzieląc masę galaktyki przez średnią masę gwiazdy w tej galaktyce. Z charakterystyki pola grawitacyjnego przy założonym równomiernym rozkładzie masy możemy uznać masę galaktyki jako masę punktową, wokół której orbituje Słońce. W porównaniu do masy galaktyki masa gwiazdy jest zaniedbywana, co daje nam wzór z III prawa Keplera w postaci:

   

Ponadto w dobrym przybliżeniu, możemy przyjąć orbitę Słońca za kołową. Zatem wykorzystując wspomniane wcześniej oszacowanie, otrzymujemy wzór na liczbę gwiazd:

   

Szacowana liczba gwiazd to 

Założenie o równomiernym rozłożeniu masy nie jest konieczne w tak silnej postaci. Ważne dla zadania jest, że środek masy wszystkich gwiazd bliżej środka galaktyki niż rozważana orbita jest zgodny z ogniskiem tej orbity.

Zadanie 2

W rozważanej sytuacji, ponieważ wiatr słoneczny nie wpływa na ruch Ziemi oraz przybliżamy orbitę do okręgu, moment pędu planety jest zachowany i wyraża się wzorem:

   

Natomiast prędkość jest stosunkiem obwodu do okresu obrotu:

   

Wyznaczając odwrotność okresu z (1) i (2) otrzymujemy:

   

Zapisując III prawo Keplera dla układu Ziemia-Słońce, można zaniedbać masę Ziemi i wzór sprowadza się wtedy do:

   

Podstawiając (3) do (4) i przekształcając, otrzymujemy zależność promienia orbity od masy Słońca:

   

   

W ciągu t lat masa gwiazdy zmaleje o , a więc wyniesie . Przy zachowaniu momentu pędu i masy Ziemi wyznaczamy stosunek nowego promienia do obecnego w zależności od utraty masy. Obustronnie odejmujemy jeden, by uzyskać, o jaki ułamek zwiększyła się jednostka astronomiczna:

   

Jednak ponieważ ubytek masy w czasie t jest zaniedbywany względem masy Słońca (12 rzędów wielkości różnicy), zmiana długość jednostki astronomicznej wynosi jedynie AU.

Zadanie 3

Pole zakreślone przez promień wodzący między apogeum a perygeum jest równe połowie pola powierzchni elipsy będącej orbitą. Z II prawa Keplera prędkość polowa na orbicie jest stała i wynosi:

   

Zatem czas t potrzebny satelicie do przebycia do perygeum jest równy połowie okresu obiegu.

Dla małych czasów możemy przybliżyć pole zakreślone przez promień wodzący jako pole trójkąta , jednocześnie przybliżając r’ jako r oraz  jako , gdzie r to długość promienia wodzącego, a  to chwilowa prędkość kątowa. Zatem w okolicach apogeum prędkość polowa wyraża się także wzorem:

   

a następnie korzystamy z faktu, że sinus małego kąta przybliża się wartością kąta w radianach:

   

Korzystając z zależności geometrycznych elipsy przyrównujemy równania (1) i (2), a następnie podnosimy do kwadratu:

   

   

Z III prawa Keplera dla satelity o pomijalnej masie orbitującej wokół Ziemi:

   

Podstawiamy (4) do (3), korzystamy z zależności :

   

   

   

Wróćmy teraz do równania (4) i wyznaczmy z niego czas t. Wykorzystamy zależność oraz (5).

   

   

   

W ten sposób uzyskaliśmy zależność, którą mieliśmy wyprowadzić.

Zadanie 4

Jeśli narysujemy prostą przez ognisko, w którym znajduje się ciało centralne ze środkiem elipsy i oznaczamy punkty przecięcia prostej z elipsą, to stosunki odległości między tymi 4 punktami są zachowane niezależnie od odległości. Poglądowe graficzne przedstawienie rzutu na podstawie podpunktu a) przedstawia rysunek poniżej. Zainteresowanych lepszą wizualizacją odsyłamy do programów takich jak GeoGebra 3D.

 

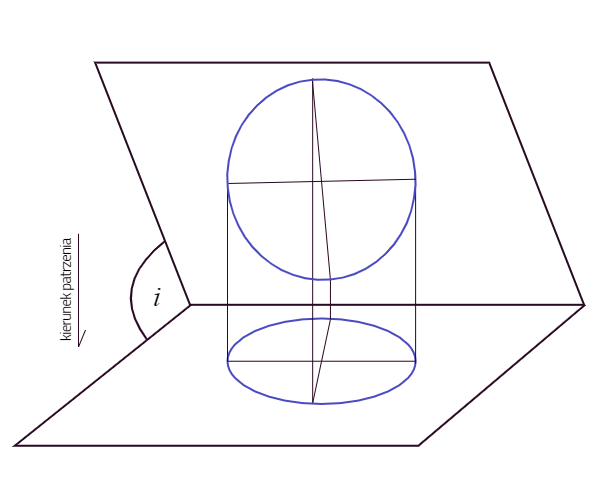
a. Gwiazda centralna (oznaczona O) znajduje się w środku obserwowanej orbity, jest zatem w środku rzeczywistej orbity. Mimośród wynosi zatem 0.

 

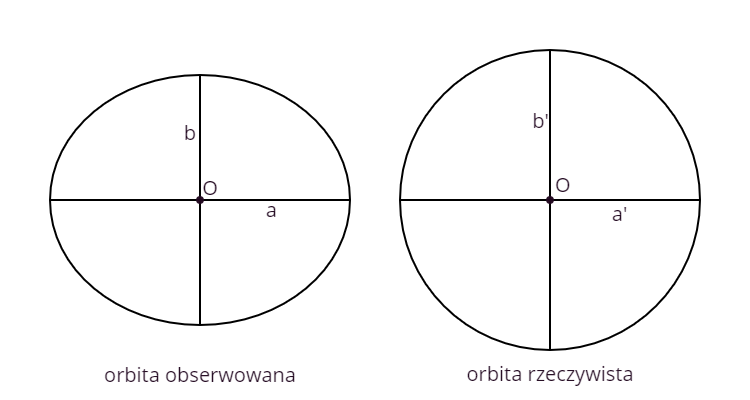
Nachylenie płaszczyzn pod kątem i powoduje “spłaszczenie” okręgu orbity przy rzutowaniu wzdłuż jednej średnicy. Z zależności rzutowania oraz , a ponieważ orbita jest okręgiem . Wartość i wynosi więc:

   

b. Gwiazda centralna (oznaczona O) leży w połowie promienia obserwowanej kołowej orbity zatem mimośród jest równy

 

Z geometrii rzutowania , oraz z geometrii elipsy wyznaczamy:

   

c. Gwiazda centralna (oznaczona O) znajduje w połowie małej półosi. Zatem mimośród wynosi .

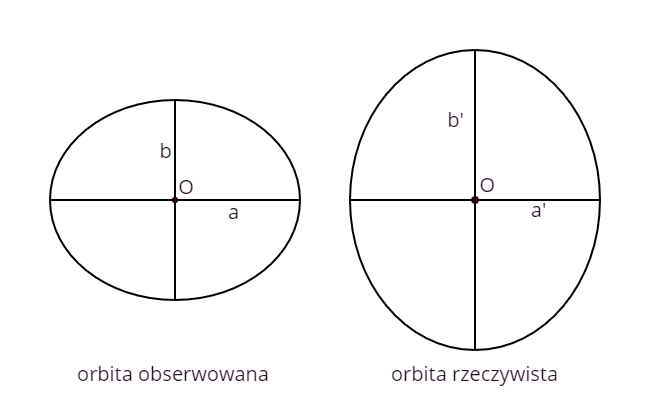
Z geometrii rzutowania , oraz z geometrii elipsy wyznaczamy:

   

Korekta – Zofia Lamęcka