Poprzednie artykuły z serii zajmowały się głównie przypadkami, w których mniejsze ciało okrąża drugie o dużo większej masie. W takiej sytuacji masę całego układu można przybliżyć masą większego obiektu. Sytuacja się jednak komplikuje, gdy masy obu obiektów są porównywalne. Taki układ nazywa się układem podwójnym. Może się on składać z dwóch gwiazd lub innych obiektów.

Istnieją też oczywiście układy, które zawierają więcej niż dwa obiekty. Jednym z przykładów jest układ Alfa Centauri, który składa się z trzech gwiazd: α Centauri A (Rigil Kentaurus), α Centauri B (Toliman) i α Centauri C (Proxima Centauri). Składniki A i B okrążają się po orbicie rzędu wielkości Układu Słonecznego, natomiast składnik C okrąża je w dużo większej odległości (~0.21 ly). Nic nie stoi na przeszkodzie, aby w układzie było jeszcze więcej składników i faktycznie spotykane są również układy z czterema i więcej gwiazdami. Nie będziemy jednak zajmować się nimi w tym artykule, ponieważ w ogólnym przypadku nie jest możliwe wyznaczenie analitycznych równań ruchu. Zainteresowanym polecam poszukać o „problemie trzech ciał” lub „n ciał”. Pewnym szczególnym przypadkiem są punkty Lagrange’a, o których można się więcej dowiedzieć w artykule Mechanika Nieba 5.

Barycentrum

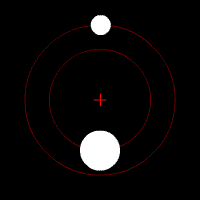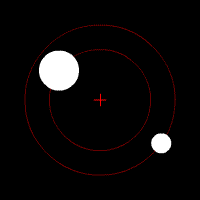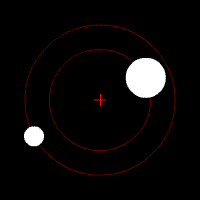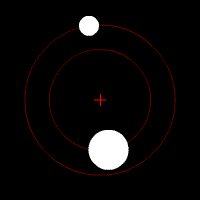
Pierwszą rzeczą, o której należy wspomnieć przy rozważaniu układów podwójnych, jest tzw. barycentrum, które jest środkiem masy układu. Nie musi ono znajdować wewnątrz obiektów, jest ono zwyczajnym punktem w przestrzeni. Jest ono również punktem, wokół którego krążą oba obiekty. Aby sobie to lepiej zobrazować, możemy sobie wyobrazić zawodnika rzutu młotem. Podczas zamachu zawodnik nie jest wyprostowany, lecz musi się wychylić do tyłu. Razem z kulą obracają się wokół barycentrum, które znajduje się w pewnym punkcie na lince, która ich łączy.

Podobnie zachowują się układy ciał, które są powiązane ze sobą siłą grawitacji. Jednym z przykładów może być układ Ziemia-Księżyc. Mimo że Księżyc ma około 100 razy mniejszą masę od Ziemi, to jednak jest to wystarczające, aby zauważalnie przesunąć barycentrum ze środka planety. Podobna sytuacja występuje w Układzie Słonecznym. Słońce posiada około 99.85% masy całego Układu, jednak przy specyficznym ułożeniu planet barycentrum może „wyjść” poza nie.

Zhatt

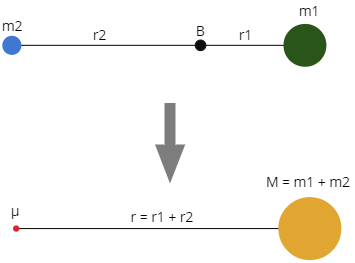
Ruch dwóch ciał wokół wspólnego środka masy.

W pierwszym artykule z mechaniki nieba dowiedzieliśmy się, jak wyznaczać środek masy układu. Dla dwóch ciał przyjmuje on postać:

Dodatkowo wiemy, że okres obrotu obu obiektów musi być równy. Mamy więc:

Po podstawieniu do wzoru na środek masy uzyskujemy zależność:

Przykład

Dla przykładu policzmy, gdzie znajduje się barycentrum układu Ziemia-Księżyc.

Gdzie to odległość od jądra Ziemi do barycentrum, to odległość od jądra Księżyca do barycentrum, a  to odległość od jądra Księżycem i do jądra Ziemią.

Po podstawieniu:

Masa Zredukowana

Ruch dwóch ciał względem siebie w układzie odniesienia barycentrum może być trudny do analizowania. Na szczęście jest metoda pozwalająca uprościć nieco sytuację. Otóż można rozważyć sytuację w układzie odniesienia jednego z obiektów. Pierwszy obiekt unieruchamiamy i badamy, jak się porusza drugie ciało względem niego. Możemy wtedy przyjąć, że ciało centralne posiada masę równą sumie obu obiektów , natomiast drugie ciało ma tzw. masę zredukowaną . Łatwo możemy zweryfikować, że ma ona jednostkę masy, a także jest mniejsza masy od każdego obiektu należącego układu, t.j. .

Michał Wójcik

Możemy również sprawdzić, że energia potencjalna układu jest taka sama, niezależnie od układu odniesienia. Energia potencjalna grawitacji obliczana jest jako . Po podstawieniu oraz  w miejsce i  otrzymujemy:

Podobnie zachowana jest również siła grawitacji, energia kinetyczna układu oraz moment pęd.

Energia właściwa i równanie vis-viva

Kilka poprawek należy również wprowadzić w równaniach na energię układu. We wcześniejszym artykule przyjęliśmy, że masa ciała centralnego jest znacznie większa i w jego układzie odniesienia energia całkowita wynosi: . Równanie to zakładało, że ciało centralne nie porusza się, więc nie posiada energii kinetycznej. Teraz już jednak wiemy, że jeśli dwa ciała mają zbliżone do siebie masy, to przy przejściu do układu odniesienia jednego z nich należy rozważyć układ o masach i . Wtedy równanie przyjmuje postać:

Chcąc uzyskać energię właściwą, należy podzielić energię całkowitą przez masę zredukowaną , zamiast przez masę jednego z obiektów:

Zmianie ulega również wzór pozwalający obliczyć energię właściwą na podstawie masy i półosi wielkiej. Wcześniej miał on postać , jednak właściwa postać dla układu podwójnego to:

Analogiczna zmiana () zachodzi w równaniu vis-viva:

Oraz w równaniu na moment pędu:

Przykładowe zadania

1. Dwie gwiazdy obiegają wspólny środek masy z okresem P = 71,91 lat. Gwiazda o masie obiega środek masy po okręgu o promieniu . Z dokładnością do  oblicz masę drugiej gwiazdy .(58 OA, II etap, zad 1)
   Wskazówka do zadania: równanie typu x = f(x) można próbować rozwiązać metodą iteracji:
2. Dwie gwiazdy ciągu głównego o masach M i m tworzyły układ podwójny o orbitach kołowych. W wyniku ewolucji bardziej masywny składnik o masie M wybuchł i wyrzucił część swojej masy () w przestrzeń międzygwiazdową. Przyjmując, że wybuch był izotropowy, a wyrzucona materia szybko opuściła układ, nie przekazując pędu drugiemu składnikowi, oblicz, jaką część swojej masy mogła utracić ta gwiazda, by nowy układ podwójny, złożony z drugiego składnika i pozostałości po pierwszym, nie uległ rozpadowi.
   Przedyskutuj, co w świetle otrzymanego wyniku można powiedzieć o ewolucji układu Syriusza, zbudowanego obecnie ze składnika A o masie oraz składnika B o masie , jeśli ocenia się, że początkowa masa Syriusza B wynosiła .(59OA, III etap, zad 1)

Rozwiązania

Zadanie 1

Zapiszmy trzecie prawo Keplera dla tego układu:

gdzie a = r_1 + r_2 jest odległością między gwiazdami.

Zapiszmy również to prawo dla układu Słońce-Ziemia:

gdzie yr oznacza lata.

Następnie podzielmy pierwsze równanie przez drugie, otrzymując:

Dzięki temu równaniu możemy łatwo ze sobą powiązać wielkości, jeśli wyrazimy je w odpowiednich jednostkach, czyli półoś w jednostkach astronomicznych, okres w latach, a masę w masach Słońca.

Następnie z zależności i , po prostych przekształceniach uzyskujemy:

Możemy to teraz podstawić do wcześniejszego wzoru:

Przenieśmy okres na prawą stronę:

Możemy teraz pomnożyć stosunek mas po lewej stronie przez :

I przenieść go na prawą stronę:

Jest to równanie z jedną niewiadomą , jednak jest ono trzeciego stopnia. Aby znaleźć rozwiązanie możemy skorzystać z wskazówki do zadania, która mówi, że można w sposób iteracyjny znaleźć rozwiązanie. Przekształćmy nasze równanie do formy x = f(x):

Po podstawieniu wartości liczbowych w odpowiednich jednostkach otrzymujemy:

Gdzie wyrażone jest w masach Słońca.

Aby rozwiązać równanie zastosujemy tzw. metodę iteracyjną. Można przy jej pomocy rozwiązywać pewne klasy równań nieliniowych od zmiennej , o ogólnej postaci:

Należy wybrać początkową wartość i podstawić ją do prawej strony równania, otrzymując wartość . Proces powtarzamy iteracyjnie:

dla kolejnych wartości ze zbioru liczb naturalnych. Metodę można zastosować jeśli rozwiązanie jest zbieżne to znaczy istnieje skończona granica ciągu .

Przykładowe zastosowanie metody iteracyjnej w naszym przykładzie:

Po około 10 wykonaniach wartość stabilizuje się na ok 3,39 , co jest rozwiązaniem zadania (z dokładnością, jaka była wymagana w treści zadania). Należy pamiętać, aby przy obliczeniach iteracyjnych zachowywać jak największą dokładność poprzedniego wyniku przy wykonaniu kolejnego kroku. Większość kalkulatorów naukowych posiada funkcjonalność wykorzystywania wyniku działań przy obliczaniu kolejnych rozwiązań, co zagwarantuje najlepszą dokładność.

Zadanie 2

Z równania vis-viva możemy obliczyć względną prędkość przed wybuchem:

Gdzie r jest odległością pomiędzy gwiazdami.

Obliczmy teraz energię układu tuż po wybuchu w układzie odniesienia jednej z gwiazd. Ponieważ wybuch był izotropowy, to nie wpłynął na prędkość wybuchającej gwiazdy. Zauważmy również, że w chwili tuż po wybuchu prędkość względna gwiazd oraz odległość między nimi są takie same, jak w chwili przed wybuchem.

Niech 

Gdzie jest masą zredukowaną.

Aby układ nie uległ rozpadowi, całkowita energia powinna być mniejsza od zera. Otrzymujemy:

Po podstawieniu wzoru na prędkość otrzymujemy:

Podstawiając :

Aby układ nie uległ rozpadowi, masa utracona w wybuchu musi być mniejsza od połowy sumarycznej masy układu przed wybuchem.

W przypadku układu Syriusza masa początkowa wynosiła , a po wybuchu , więc układ stracił ponad połowę początkowej masy. Ponieważ układ nie rozpadł się, to należy wnioskować, że nie zostało spełnione któreś z założeń zadania, to znaczy wybuch mógł nie być izotropowy i wpłynąć na prędkość wybuchającej gwiazdy lub część wyrzuconej materii mogła przekazać pęd drugiemu składnikowi.