Mechanika nieba 1: Wprowadzenie do grawitacji

Posted on 16 czerwca 202118 stycznia 2022 by Michał Stefanik 7k odsłon

W paru kolejnych artykułach postaramy się przybliżyć naturę oddziaływania grawitacyjnego według fizyki klasycznej. Nie będziemy tu poruszać teorii względności Einsteina. Aby zrozumieć większość poruszanych w tym dziale zagadnień, potrzebna jest znajomość matematyki i fizyki na poziomie liceum. Jednak w przypadku niektórych znajomość analizy matematycznej wielokrotnie może okazać się przydatna lub nawet niezbędna.

Dlaczego mechanika klasyczna?

Może słyszeliście kiedyś o teorii względności, czy mechanice kwantowej. W astronomii również mają one swoje zastosowanie, jednak dużo prościej korzystać z klasycznych wzorów. Są one na tyle dokładne, że korzystanie z innych teorii ma sens dopiero przy ekstermalnych warunkach. Zachowanie się przestrzeni w pobliżu czarnych dziur lub gwiazd neutronowych to niektóre z przypadków. Do obliczania okresu obrotu planety wokół gwiazdy najczęściej wystarczą prawa Newtona i Keplera. Jednak abyśmy się dobrze rozumieli, wprowadźmy parę przydatnych terminów.

Środek masy

Punkt, który często bywa rozważany jako początek układu współrzędnych lub zastępuje się nim ciała fizyczne. Środek masy to punkt w przestrzeni wyznaczony przez rozkład masy w danym ciele lub względne położenie kilku ciał. Często będziemy utożsamiać obiekty fizyczne z punktami materialnym, zaniedbując ich rozmiary. Jeśli chcemy obliczyć środek masy układu ciał, zastosujemy wzór:

$\vec{r}_{0}=\frac{\sum_{i=1}^{n}\vec{r}_{i}m_{i}}{\sum_{i=1}^{n} m_{i}}$

Jeśli jednak nasz obiekt jest “ciągły” i nie można w nim wyróżnić konkretnych punktów skupienia masy, zastosujemy wzór:

$\vec{r}_{0} = \frac{1}{M} \int \rho \vec {r} dV$

$M = \int_{V} \rho dV$

Zazwyczaj obiekty, dla których przeprowadzamy obliczenia, można potraktować jako punkt, jednak niektórych zadań bez zrozumienia powyższych wzorów nie rozwiążemy.

Michał Stefanik

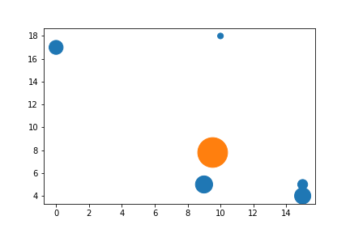
Pomarańczowy punkt wyznacza środek masy układu złożonego z niebieskich ciał. Rozmiary są proporcjonalne do masy ciała.

Michał Stefanik

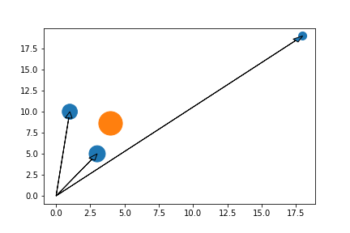
Na tym wykresie dodatkowo umieszczone zostały wektory położenia ciał. Początek układu współrzędnych jest dowolny. W tym wypadku został wybrany punkt (0, 0).

W większości przypadków będziemy brać pod uwagę ciała traktowane jako punkty materialne. Czasem jednak będzie potrzeba by skorzystać ze wzoru całkowego. Poniżej przedstawiam przykład takiego rozwiązania.

Przykład

Oblicz środek masy jednorodnej bryły ograniczonej przez powierzchnie x = 0, y = 0, z = 0, x² + y² + z² = a².

Możemy zauważyć, że dana bryła to jedna ósma kuli. Do obliczenia jej środka masy potrzebujemy znać jej moment statyczny względem jednej z głównych płaszczyzn np. wyznaczanej przez osie x i y.

$M_{XY} = \iiint_{V} \rho z\, dV$

Granice całkowania łatwiej rozpatrzyć w układzie współrzędnych sferycznych, więc takie przyjmiemy. Dodatkowo wyliczamy jakobian przejścia zmiennych $|J|$ .

$x = r \, \sin\theta \,\cos\phi$

$y = r \, \sin\theta \,\sin\phi$

$z = r \, \cos\theta$

$|J| = r^2\, \sin\theta$

Po zamianie zmiennych wyrażenie do całkowania ma postać:

$M_{XY} = \int_{0}^{\frac{\pi}{2}} d\phi \int_0^{\frac{\pi}{2}}d\theta\int_0^a \rho r\cos\theta \cdot r^2\sin\theta dr$

$M_{XY} = \rho\int_{0}^{\frac{\pi}{2}} d\phi \int_0^{\frac{\pi}{2}}d\theta\int_0^a \frac{r^3\sin(2\theta)}{2} dr$

$M_{XY} = \frac{a^4\rho}{8}\int_{0}^{\frac{\pi}{2}} d\phi \int_0^{\frac{\pi}{2}} \sin(2\theta)d\theta$

$M_{XY} = \frac{a^4\rho}{8}\int_{0}^{\frac{\pi}{2}} \Big[\frac{-\cos(2\theta)}{2}\Big]\Big|_0^{\frac{\pi}{2}} d\phi$

$M_{XY} = \frac{a^4\rho}{8}\int_{0}^{\frac{\pi}{2}} d\phi$

$M_{XY} = \frac{a^4\rho\pi}{16}$

Wiemy, że rozważana bryła to część jednorodnej kuli. Masa tej bryły będzie wynosić $\frac{1}{8}\cdot \frac{4}{3}\pi a^3$ . Bryła jest symetryczna, więc momenty statyczne względem pozostałych płaszczyzn pozostaną takie same. Ostatecznie współrzędne wynoszą $x_0 = y_0 = z_0 = \frac{M_{XY}}{M} = \frac{3}{8}a$ .

Prawa Dynamiki

Sir Isaac Newton wprowadził 3 zasady. W skrócie mówią one o tym, że:

Jeśli siły działające na ciało się równoważą, to ciało to nie zmienia swojej prędkości
Jeśli na ciało działa siła, to wywołuje ona przyspieszenie równe $\vec{a} = \frac{\vec{F}}{m}$ . Inaczej $\vec{F}=\frac{d\vec{p}}{dt}$
Jeśli ciało $m_1$ oddziałuje na ciało $m_2$ , to ciało $m_2$ oddziałuje na ciało $m_1$

Inne ważne prawa to prawa zachowania. Znaczy to, że pewne wartości dla danego układu pozostają niezmienne np. energia, czy pęd.

Siła grawitacji

Grawitacja to zjawisko naturalne powodujące, że dwa ciała posiadające masę się przyciągają. Siła tego oddziaływania opisywana jest wzorem:

$\vec{F} = G\frac{m_1m_2}{|\vec{r}|^2}\frac{\vec{r}}{|\vec{r}|}$

Jest więc bezpośrednio zależna od masy obu ciał, a także od odległości między nimi. G to stała grawitacyjna wyznaczona eksperymentalnie. Pole sił grawitacyjnych podlega zasadzie superpozycji, co znaczy, że siła wypadkowa działająca na ciało A od innych ciał układu, będzie sumą sił od poszczególnych ciał. Ponadto każde z ciał danego układu oddziałuje ze wszystkimi innym. Siła działająca na ciało A przez B ma taką samą wartość jak siła wywoływana przez A na B.

Michał Stefanik

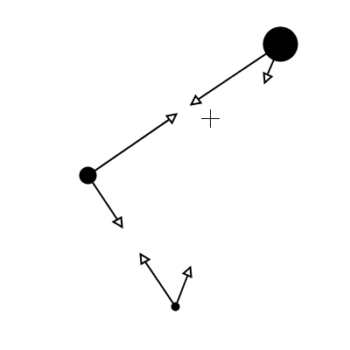
Punkty na rysunku reprezentują ciała. Promień punktu jest proporcjonalny do jego masy (stosunki mas 1:2:3). Krzyżykiem zaznaczono środek masy układu.

Oprócz samej siły możemy rozważać wpływ danego ciała (lub układu ciał) na przestrzeń rozciągającą się wokół niego. Będzie to natężenie pola grawitacyjnego.

$\vec\gamma = G\frac{m_1}{|\vec{r}|^2}\frac{\vec{r}}{|\vec{r}|}$

Jest ono stosunkiem siły oddziałującej na ciało podzielonym przez jego masę. Inaczej, jest przyspieszeniem nadawanym ciału leżącemu w odległości r od ciała m₁.

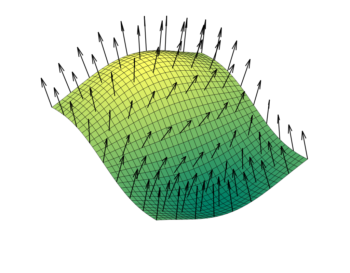
W niektórych przypadkach może okazać się przydatne prawo Gaussa. Przed jego treścią musimy jeszcze wprowadzić wektor powierzchni $\vec S$ . Jest on prostopadły do powierzchni, a jego wartość jest równa polu powierzchni. Na poniższym obrazku przedstawione są takie wektory.

By Nicoguaro - Own work, CC BY 4.0

Powierzchnia z zaznaczonymi wektorami normalnymi.

Prawo Gaussa w postaci całkowej ma postać:

$\oint_{S}\vec{\gamma}\cdot d \vec S = 4\pi GM$

Mówi ono, że gdyby otoczyć masę pewną powierzchnią, podzielić ją na małe pola, i dla każdego z tych pól wyliczyć ile natężenia grawitacyjnego do niego wpada, to okazałoby się, że dla dowolnej powierzchni wynik ten będzie taki sam i będzie wynosił właśnie $4 \pi GM$ . W najprostszym przypadku, gdyby punkt o masie $M$ otoczyć sferą o promieniu $R$ lewa strona równania będzie mieć postać $G\frac{M}{R^2}\cdot 4\pi R^2$ .

Jeszcze jedna ważna uwaga. Rozważając siłę pochodzącą od ciała o sferycznej symetrii, patrząc z zewnątrz, można uznać, że cała masa danego ciała jest skupiona w jednym punkcie. Dla dociekliwych dowód można znaleźć tutaj.

Prędkości kosmiczne

Znając prędkość pewnego ciała w danym układzie, jesteśmy w stanie stwierdzić jaką orbitę obierze dane ciało. Szczególne znaczenie mają dwie prędkości zwane prędkościami kosmicznymi. Pierwsza prędkość kosmiczna jest prędkością, którą musi mieć ciało, by obiegać masę M na orbicie kołowej. Wartość pierwszej prędkości kosmicznej możemy wyznaczyć, przyrównując siłę grawitacji do siły dośrodkowej. Często pod promień podstawia się promień samego ciała niebieskiego, by wiedzieć, jaka jest minimalna prędkość kosmiczna. W związku z tym często będziemy ją rozumieć jako prędkość ciała na orbicie kołowej przy powierzchni ciała.

$G \frac{Mm}{R^{2}} = \frac{mv^{2}}{R}$

$v_{1} = \sqrt{\frac{GM}{R}}$

Druga prędkość kosmiczna, to prędkość, przy której energia ciała jest tak duża, że oddziaływanie grawitacyjne nie może już tego ciała zatrzymać. Jego orbita będzie miała kształt paraboli, a każda większa prędkość sprawi, że orbita stanie się hiperbolą. W układzie dwóch ciał oznacza to, że ciała takie zbliżą się do siebie tylko raz. Prędkość ta wiąże się z wartością energii całkowitej ciała na orbicie. Energia ta w tym granicznym przypadku wynosi 0, więc suma energii kinetycznej i potencjalnej grawitacji również wynosi 0. Tę drugą omówimy dokładniej w kolejnych artykułach.

$\frac{mv^2}{2} - \frac{GMm}{R} = 0$

$v_2 = \sqrt{\frac{2GM}{R}}$

Przykładowe zadania

Jaką masę, przy zachowaniu rozmiarów i odległości, musiałby mieć Księżyc, by stojący “pod Księżycem” na Ziemi człowiek odczuwał bezwładność? Za masę Ziemi przyjmij 5,97×10²⁴ kg, promień Ziemi 6,4×10⁶m oraz odległość środków ciężkości Księżyca od Ziemi 2,4×10 ⁹
Mając trzy ciała o położeniach (13, 13), (12, 0), (18, 6) oraz masach 10, 30, 25, wyznacz ich środek ciężkości.
Znajdź wartość pierwszej prędkości kosmicznej na Marsie. Przyjmij G = 6,67 × 10^–11 N × m²/kg², M_M = 6,39 × 10²³ kg, promień Marsa R = 3,4 × 10⁶ m.
Oszacuj masę gromady kulistej, w której średni kwadrat prędkości wynosi 3 km/s, a promień wynosi 20 pc.

Rozwiązania

Zadanie 1

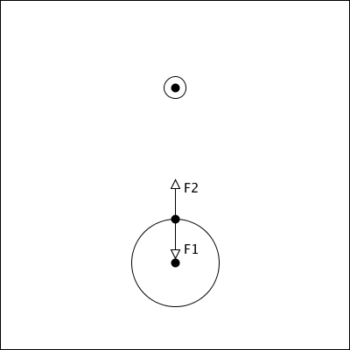
Hipotetyczną sytuację z zadania pierwszego ilustruje poniższy rysunek. W pogrubionym punkcie znajduje się człowiek, większe koło reprezentuje Ziemię, mniejsze księżyc. Skoro jest w stanie nieważkości to siła $F_{1}$ wywierana przez Ziemię ma równoważyć siłę $F_{2}$ wywieraną przez Księżyc.

Michał Stefanik

Rysunek do zadania 1.

$F_{1} = F_{2}$

$\frac{GM_{Z}m}{R_{Z}^{2}} = \frac{GM_{K}m}{R_{K}^{2}}$

$M_{K} = M_{Z}\frac{R_{K}^{2}}{R_{Z}^{2}}$

$R_{K} = d_{ZK} - R_{Z}$

$M_{K} = 8,35 10^{29} kg$

Zadanie 2

W zadaniu po prostu skorzystamy z podanego wcześniej wzoru.

$\vec{r}_{0}=\frac{\sum_{i=1}^{n}\vec{r}_{i}m_{i}}{\sum_{i=1}^{n} m_{i}}$

$\vec{r}_{0} = \frac{[13, 13]\cdot10 + [12, 0]\cdot30 + [18, 6]\cdot25}{10 + 30 + 25}$

$\vec{r}_{0} = [14.46153846, 4.30769231] [m]$

Zadanie 3

By rozwiązać to zadanie, wystarczy skorzystać ze wzoru na pierwszą prędkość kosmiczną, podstawiając podane dane. Otrzymany wynik to około 3,5 km/s.

Zadanie 4

Na gromadę kulistą spojrzymy jak na pewien zbiór masy. Wszystkie orbitujące wokół jej środka masy ciała również podlegają prawom zachowania energii. Jeśli więc znamy jej promień i średni kwadrat prędkości, możemy uznać, że jest to w jakimś stopniu przybliżenie drugiej prędkości kosmicznej. Przekształcając wzór na tę prędkość, obliczamy szacowaną masę gromady. Tym przybliżeniem dostaniemy masę równą około 8 × 10³⁴ kg.

Źródła:

NASA
Zbiór zadań z Olimpiad Astronomicznych XXVI - XXXV
A Problem book inAstronomy and Astrophysics

Tagi

Dlaczego mechanika klasyczna?

Środek masy

Przykład

Prawa Dynamiki

Siła grawitacji

Prędkości kosmiczne

Przykładowe zadania

Rozwiązania

Zadanie 1

Zadanie 2

Zadanie 3

Zadanie 4

Tagi

Olimpiada Astronomiczna Juniorów

Rusza druga edycja Olimpijskiej Ligi Astronomicznej

Sukces Polaków na Międzynarodowej Olimpiadzie Astronomicznej 2024 w Brazylii

Jak działa teleskop?