Część druga artykułu traktującego o orbitach z punktu widzenia astronautyki. Tym razem „na warsztat” bierzemy orbity eliptyczne.
Przypadek orbity kołowej jest, jak zostało to wspomniane w poprzedniej części, bardzo wyidealizowany. Wartość prędkości i wysokość muszą być dokładnie skorelowane, a kierunek prędkości dokładnie poziomy. Możemy się domyślać, że ta sytuacja właściwie nie występuje naturalnie, a jest również trudna do osiągnięcia przez sztuczne satelity ze względu na błędy pomiarowe oraz niedokładności wykonywania manewrów. Dlatego też, aby naprawdę zrozumieć co dzieje się z satelitami, potrzebujemy zrozumienia istoty orbity, która nie będzie obłożona tyloma warunkami. Z pomocą przychodzi nam pierwsze prawo Keplera, które w brzmieniu oryginalnym mówi, że planety wokół Słońca poruszają się po elipsach, a Słońce znajduje się w jednym z ognisk tej elipsy. Prawo to zostało odkryte na podstawie obserwacji i było jednym z dowodów na poprawność teorii grawitacji Newtona, z której eliptyczny kształt orbity wynika wprost. Wiadome jest więc, że prawo to nie może dotyczyć tylko planet i Słońca, ponieważ siła grawitacji występuje pomiędzy dowolnymi dwoma ciałami posiadającymi masę. Dlatego właśnie elipsa jest tak ważną krzywą, ponieważ każdy satelita o masie znacznie mniejszej od masy ciała centralnego będzie poruszał się w jego polu grawitacyjnym właśnie po elipsie. Wciąż obowiązują nas pewne obostrzenia, mianowicie satelita ten musi mieć prędkość mniejszą niż ta pozwalająca na ucieczkę z tego pola grawitacyjnego oraz nie może na niego działać żadna siła za wyjątkiem siły grawitacji pochodzącej od ciała centralnego. Z pierwszym z tych założeń rozprawimy się w dalszej części artykułu, natomiast drugie z nich zostanie omówione w tym cyklu w kontekście manewrów orbitalnych, czyli sytuacji, w której używamy napędu w celu zmiany orbity.
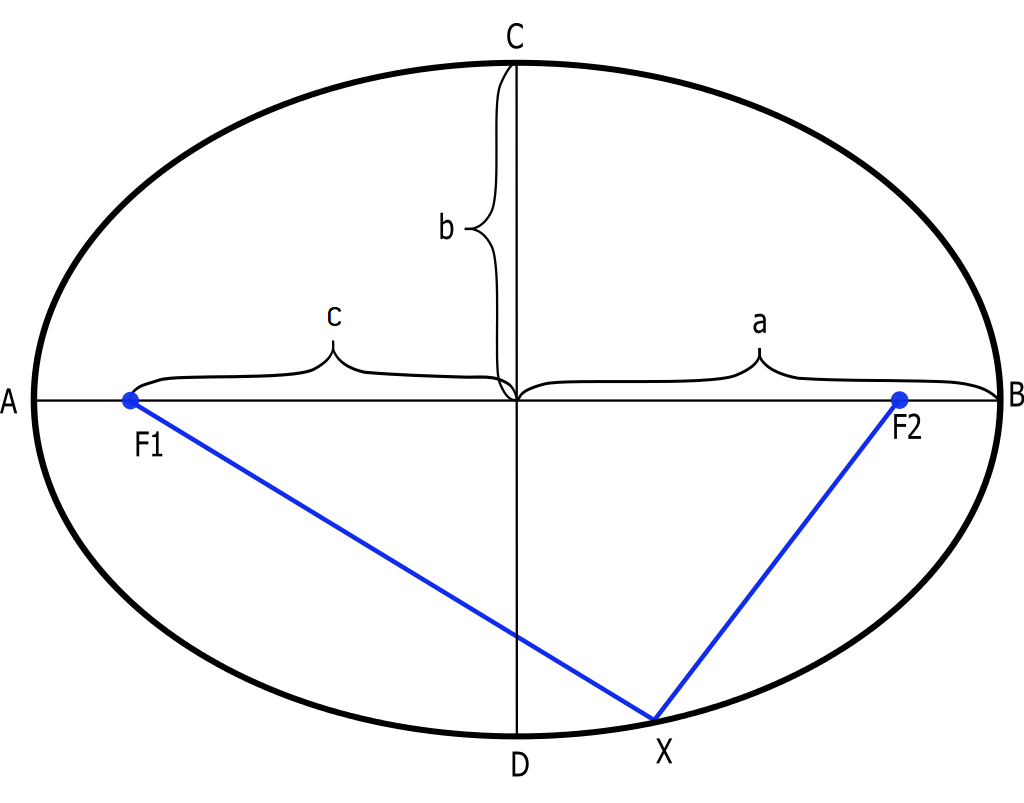
Rys. 1: Rysunek elipsy z zaznaczonymi ważnymi odcinkami i punktami.
W tym miejscu chciałbym omówić pewne istotne właściwości geometryczne elipsy, które pozwolą lepiej zrozumieć problem najistotniejszych orbit w astronautyce. Jestem bowiem świadomy, że wielu czytelników mogło się z tą krzywą nie spotkać w ogóle lub tylko w bardzo ograniczonym zakresie. W szkole na matematyce nie jest ona zwykle wprowadzana, a na fizyce mówi się o niej jedynie jakościowo. Spójrzmy zatem na Rys. 1, na którym widzimy elipsę z zaznaczonymi najważniejszymi jej elementami. Rozpocznijmy najpierw od jednej z kilku równoważnych definicji elipsy — jest to krzywa będąca zbiorem punktów, których suma odległości od ognisk jest stała. Ta suma odległości jest równa tak zwanej wielkiej osi elipsy (2*a na Rys. 1). Łatwo uświadomić sobie ten fakt rozważając punkty leżące najbliżej ognisk elipsy w kontekście przytoczonej definicji. Połowę wielkiej osi nazywamy wielką półosią i wraz z małą półosią (b na Rys. 1) mogą być one użyte do pełnego zdefiniowania elipsy. Okazuje się to jednak zwykle dość niewygodne i dlatego używamy połowy odległości między ogniskami (c na Rys. 1), aby zdefiniować mimośród:
(1)
Jest to miara spłaszczenia elipsy — gdy przyjmuje wartość 0, krzywa ta jest tożsama z kołem. Dla elips mimośród zawsze jest mniejszy od 1. Opis elipsy za pomocą wielkiej półosi i mimośrodu lub za pomocą małej i wielkiej półosi jest równoważny, a zależność pozwalająca przechodzić z jednego do drugiego jest twierdzeniem Pitagorasa dla trójkąta o wierzchołkach w ognisku, środku elipsy i punkcie na krzywej znajdującym się także na małej półosi (polecam zastanowić się, dlaczego ta zależność jest prawdziwa, mając w głowie przytoczone już własności elipsy, zwłaszcza jej definicję):
(2)
Ostatnią istotną własnością, chociaż może niezbyt ważną z punktu widzenia tego artykułu, jest konstrukcja stycznej do elipsy. Jak pomocna może to być konstrukcja wiedzą na pewno Ci, którzy pamiętają, że prędkość ciała zawsze jest styczna do jego toru ruchu, dlatego też rozważając orbity, nie sposób o tym nie wspomnieć. Otóż okazuje się, że styczna do elipsy jest po prostu dwusieczną kąta między prostymi poprowadzonymi z danego punktu na krzywej przez ogniska (patrz Rys. 2). Dowód tej własności dociekliwy czytelnik może przeprowadzić samodzielnie lub znaleźć go w źródłach.
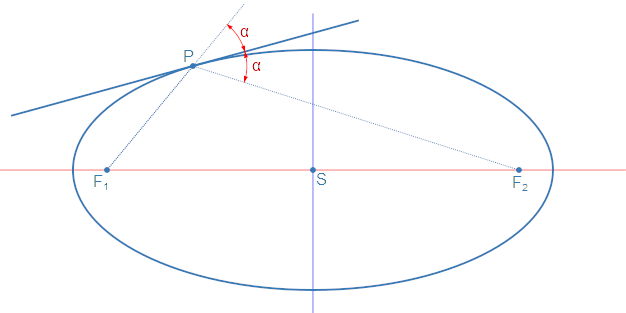
Rys. 2: Ilustracja sposobu konstrukcji stycznej do elipsy w danym punkcie.
Teraz jesteśmy gotowi do przeanalizowania i zrozumienia orbit eliptycznych. Jak już wiemy, są one uogólnieniem orbit kołowych, wróćmy więc Rys. 3 (z poprzedniej części) przedstawiającego eksperyment myślowy zwany działem Newtona i zastanówmy się, co się stanie gdy zwiększymy jeszcze bardziej prędkość początkową ciała, już po tym jak pozwala nam ona na osiągnięcie orbity kołowej. Domyślamy się, że krzywizna naszego toru nie będzie już dopasowana do krzywizny Ziemi — będzie mniejsza, stąd początkowo zaczniemy się oddalać od jej powierzchni, ale jednocześnie zaczniemy zwalniać, ponieważ siła grawitacji już nie będzie działała dokładnie prostopadle do naszej prędkości. W końcu dotrzemy do punktu gdy znajdziemy się najdalej od Ziemi i symetrycznie do pierwszej połowy toru ruchu trafimy do miejsca początkowego — podobnie jak to miało miejsce w przypadku skoku prosto w górę, tyle że tym razem w międzyczasie uda nam się okrążyć Ziemię. Już wiemy, że krzywa którą „narysujemy” będzie elipsą, a środek masy Ziemi będzie w ognisku tej elipsy (oznaczona jako D na Rys. 3), jednak dzięki tej intuicji od razu możemy też powiedzieć, że najwyższa prędkość wystąpi na samym początku naszego ruchu, które jest w tym wypadku perycentrum naszej orbity (czyli miejscem gdy znajdujemy się najbliżej Ziemi, zwanym też perygeum w przypadku orbit okołoziemskich). Najniższa prędkość osiągnięta będzie dokładnie po drugiej stronie Ziemi, gdy znajdujemy się od niej najdalej. To miejsce nazywamy apocentrum lub, w przypadku orbit okołoziemskich, apogeum. W ten oto sposób można zrozumieć istotę drugiego prawa Keplera, które mówi, że prędkość polowa ciała na orbicie jest stała. To znaczy, że odcinek poprowadzony od ciała centralnego do ciała orbitującego zakreśla równe pola w takich samych przedziałach czasu. To, że z tego prawa wynika, że w perycentrum prędkość ciała jest najwyższa, a w apocentrum najniższa dobrze ilustruje Rys. 4.
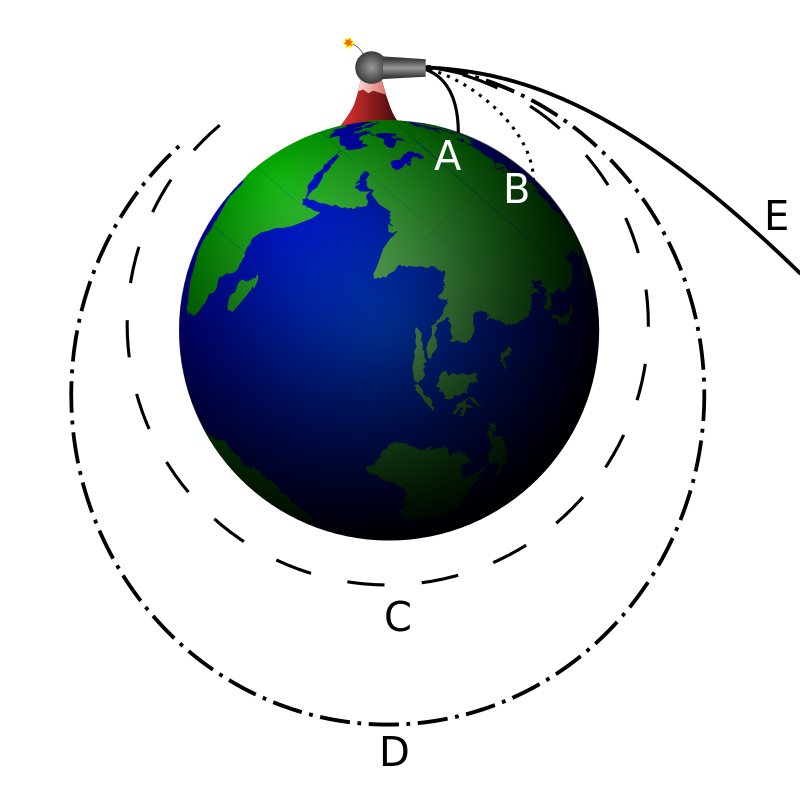
Rys. 3: Zobrazowanie eksperymentu myślowego nazywanego działem Newtona.
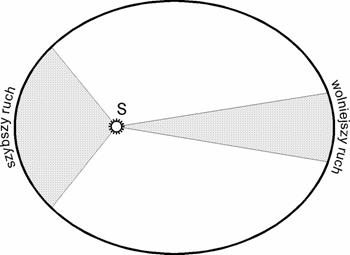
Rys. 4: Ilustracja drugiego prawa Keplera.
Po wspomnieniu o drugim prawie Keplera nie sposób nie wspomnieć również o trzecim. W naszym przypadku najbardziej użyteczna i najwięcej mówiąca jego forma wygląda następująco:
(3)
W równaniu tym a jest wielką półosią orbity, a T okresem obiegu ciała orbitującego wokół ciała centralnego. Przedstawiony iloraz jest stały dla wszystkich orbit wokół danego ciała centralnego. Widzimy więc, że im wyższa orbita, tym więcej czasu potrzeba na jeden obieg. Skoro więc omówiliśmy to, czym jest orbita eliptyczna oraz jakie prawa i wielkości są dla niej ważne, możemy zagłębić się w to, co oznaczają podawane w opisach misji kosmicznych liczby. Pierwszą ważną i budzącą czasem zdziwienie informacją jest fakt, jak najczęściej opisuje się elipsę, która ma być docelową orbitą satelity. Już wiemy, że potrzeba 2 liczb, jednak w astronautyce przyjęto używać wcale nie wielkiej półosi i mimośrodu, a raczej wysokości apocentrum i perycentrum. Wysokość jest tu rozumiana jako odległość satelity od punktu znajdującego się na powierzchni referencyjnej Ziemi dokładnie pod nim. Najczęściej stosuje się opis kształtu Ziemi z systemu WGS-84. Tak więc orbita oznaczona 400×600 to taka, której perycentrum znajduje się 400 km, a apocentrum 600 km nad powierzchnią Ziemi. Czytelnik może łatwo zauważyć, że znając lokalny promień Ziemi (na podstawie przyjętego kształtu), możemy łatwo przeliczyć podawane dwie liczby i znaleźć na przykład wielką półoś i mimośród.
Jednakże w rzeczywistości poruszamy się w przestrzeni trójwymiarowej, a nie jak dotychczas rozważane orbity na płaszczyźnie, stąd oprócz dwóch liczb opisujących elipsę, aby jednoznacznie opisać orbitę, należy dodatkowo określić:
- inklinację orbity (i na Rys. 5), czyli kąt między płaszczyzną orbity a płaszczyzną odniesienia (dla orbit okołoziemskich jest to zwykle płaszczyzna równika),
- długość węzła wstępującego (Ω na Rys. 5), czyli kąt między punktem Barana (arbitralnie wybraną osią OX układu współrzędnych związanego z gwiazdami stałymi) a miejscem, gdzie satelita przechodzi znad półkuli południowej nad północną (w przypadku orbit okołoziemskich),
- argument perycentrum (ω na Rys. 5), czyli kąt między węzłem wstępującym a perycentrum orbity,
- anomalię prawdziwą (ν na Rys. 5), czyli kąt między perycentrum a satelitą w danej chwili.
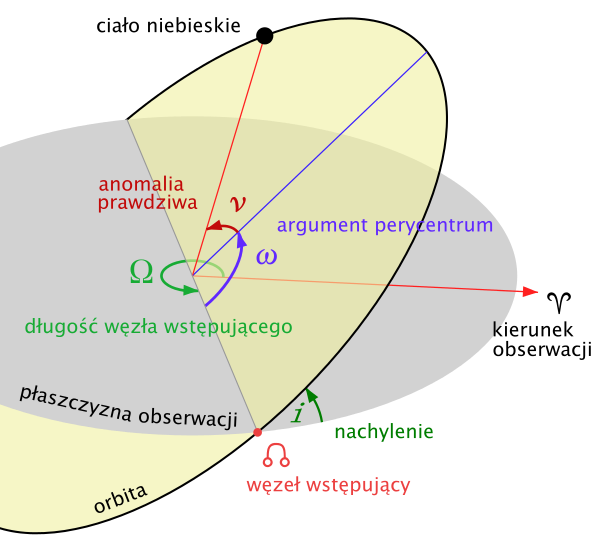
Rys. 5: Ilustracja elementów orbitalnych.
Dobrym ćwiczeniem wyobraźni przestrzennej jest wyobrażenie sobie jaka rodzina orbit byłaby opisywana przez elementy jeżeli pominęlibyśmy jeden z nich, innymi słowy jak moglibyśmy orbitą „poruszać” gdybyśmy nie zdefiniowali jej poprzez wszystkie 6 elementów. Przykładowo, niezdefiniowanie długości węzła wstępującego sprawia, że moglibyśmy ją obracać wokół osi prostopadłej do płaszczyzny odniesienia. Podobnie, niezdefiniowanie argumentu perycentrum powodowałoby możliwość obracania orbity w jej płaszczyźnie. Często nasuwa się tu pytanie, czy anomalia prawdziwa jest „pełnoprawnym” elementem orbitalnym — w końcu jest ona inna dla każdej chwili czasu. Odpowiedzieć na takie pytanie można myśląc o tak zwanej orbicie geostacjonarnej, czyli takiej, której okres obiegu jest równy okresowi obrotu Ziemi wokół jej osi. Satelity na takiej orbicie pozostają w spoczynku względem Ziemi, czyli widoczne są cały czas w zenicie nad jednym punktem na równiku. Widać, że zdefiniowanie ile wynosi anomalia prawdziwa w pewnej umówionej chwili czasu, powie nam, nad jakim punktem ten satelita będzie widoczny. Jest więc bardzo istotnym parametrem i jedynym, który odróżnia orbity satelitów geostacjonarnych od siebie.
To już koniec tej części artykułu, w następnej zajmiemy się pozostałymi przypadkami orbit — paraboliczną i hiperboliczną.
Trzecia część cyklu dostępna tutaj.




