II Olimpijska Liga Astronomiczna: Zadanie 4 z 3 serii

Treść

Jasności (M) i okresy pulsacji (P) cefeid klasycznych można powiązać zależnością $M=a\cdot\log_{10}(P)+b$ . Na podstawie danych w poniższej tabeli wyznacz współczynniki $a$ i $b$ . Niepewności można pominąć.

Gwiazda	Okres pulsacji $P$	Jasność absolutna $M$	$\log_{10}(P)$
$\ell$ Car	35,56	-5,22	1,550962
$\zeta$ Gem	10,148	-4,1	1,006380
$\beta$ Dor	9,843	-3,91	0,993127
W Sgr	7,59	-3,76	0,880242
X Sgr	7,013	-2,85	0,845904
Y Sgr	5,774	-2,06	0,761477
$\delta$ Cep	5,366	-3,47	0,729651
FF Aql	4,47	-3,4	0,650308
T Vul	4,335	-3,19	0,636989
RT Aur	3,728	-3,09	0,571476
SV Vul	44,98	-6,04	1,653019
WZ Sgr	21,83	-5,06	1,339054
S Nor	9,75	-3,95	0,989005
SU Cas	1,95	-1,99	0,290035
$\alpha$ UMi	5,75	-3,42	0,759668

Obserwujemy układ podwójny złożony z Cefeidy i towarzyszącej jej gwiazdy. Obie krążą po kołowych orbitach wokół wspólnego środka masy z okresem 2 lat, jak pokazano na rysunku. Oś obrotu układu jest nachylona o $60^\circ$ względem linii wzroku obserwatora, a szerokość kątowa odległości między gwiazdami wynosi $0{,}1^{''}$ .

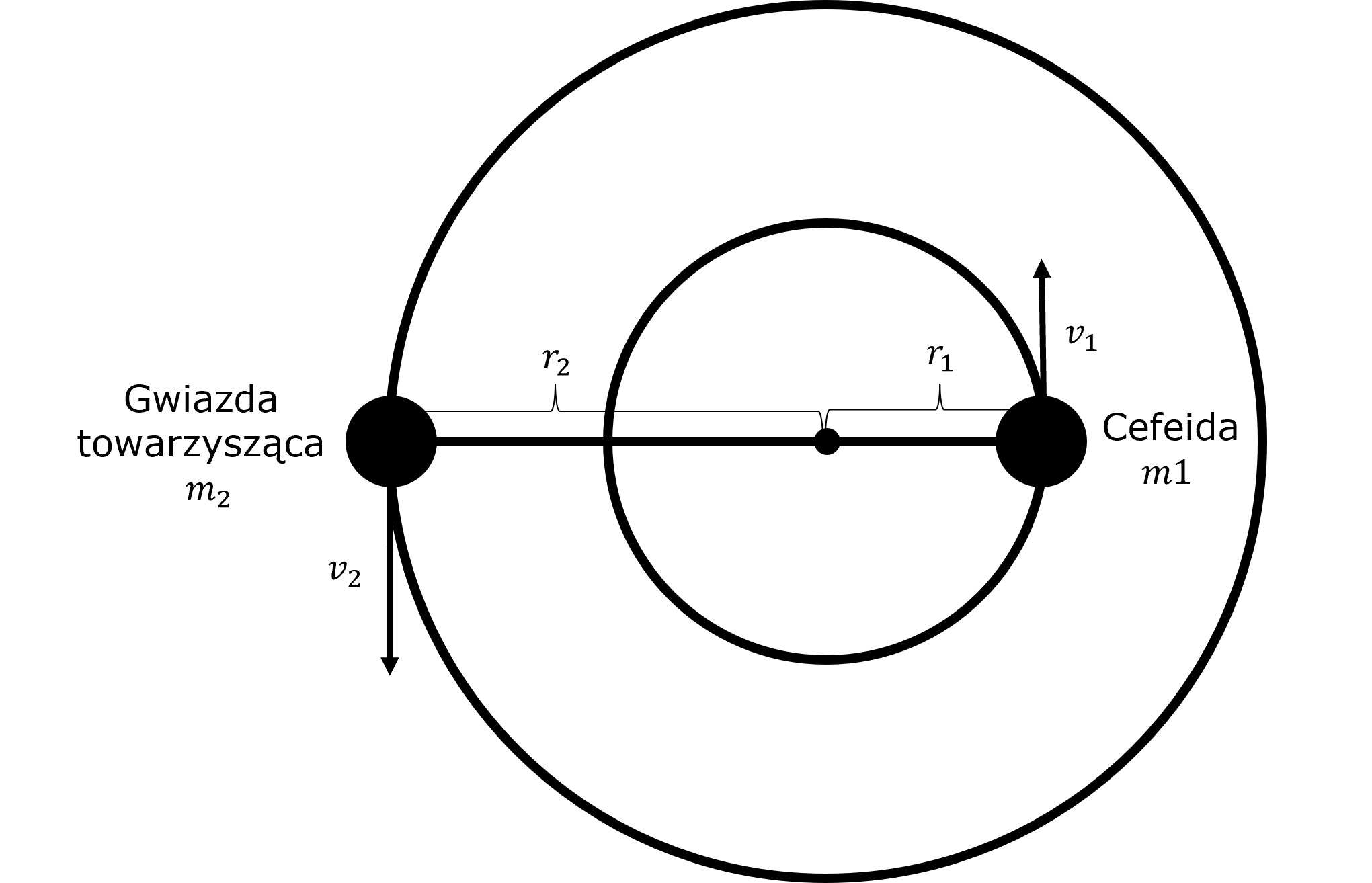
Cefeida ma jasność 5 magnitudo i pulsuje z okresem 10 dni. Obserwowana przez nas fala wyemitowana przez gwiazdę towarzyszącą jest w wyniku rotacji wokół środka masy przesunięta o $0{,}02$ nm względem fali o długości $656{,}3$ nm. Na podstawie wcześniej wyprowadzonej zależności i powyższych danych oblicz masy obu gwiazd.

Rozwiązanie

Zacznijmy od wyznaczenia zależności okres–jasność. Z tabeli wartości dopasowujemy prostą:

$M = a \log_{10} P + b,$

skąd otrzymujemy wartości $a \approx -2,766,\, b \approx -1,182.$
Następnie możemy wyznaczyć jasność absolutną Cefeidy Dla $P = 10\ \text{d}$ mamy $\log_{10} P = 1$ . Stąd

$M = a\cdot 1 + b \approx -3,948.$

Z wzoru Pogsona dla jasności absolutnej możemy teraz wyznaczyć odległość do układu. Z modułu odległości:

$m - M = 5 \log_{10}\!\left(\frac{d}{10\ \text{pc}}\right),$

dla $m = 5$ i $M = -3,948$ otrzymujemy

$d \approx 616\ \text{pc}.$

Wiemy, że kątowa separacja gwiazd to $\theta = 0,1''$ . W radianach wynosi ona

$\theta = 0,1 \cdot \frac{\pi}{180\cdot 3600}.$

Stąd separacja liniowa to

$a = \theta \cdot d \approx 61,6\ \text{AU}.$

Przejdźmy do prędkości orbitalnej gwiazdy towarzyszącej. Wiemy, że możemy ją znaleźć na podstawie przesunięcia linii widmowej:

$v_{\mathrm{rad}} = c \frac{\Delta\lambda}{\lambda_0} = 3,0\cdot 10^8 \cdot \frac{0,02}{656,3} \approx 9,14\ \text{km/s}.$

Przy kącie nachylenia $\alpha = 60^\circ$ :

$v_2 = \frac{v_{\mathrm{rad}}}{\sin\alpha} \approx 10,55\ \text{km/s}.$

Promień orbity względem środka masy:

$r_2 = \frac{v_2 P}{2\pi},$

gdzie $P = 2\ \text{lata} = 6,31\cdot 10^7\ \text{s}$ . Stąd

$r_2 \approx 0,71\ \text{AU}.$

Z trzeciego prawa Keplera możemy znaleźć całkowitą masę układu:

$M_{\mathrm{tot}} = \frac{4\pi^2 a^3}{G P^2}.$

Po podstawieniu $a = 61,6\ \text{AU}$ i $P = 2\ \text{lata}$ otrzymujemy

$M_{\mathrm{tot}} \approx 5,85\cdot 10^4 M_\odot.$

Ze związku $r_2 = a \frac{m_1}{M_{\mathrm{tot}}}$ dla środka masy:

$m_1 = M_{\mathrm{tot}} \frac{r_2}{a},\qquad m_2 = M_{\mathrm{tot}} - m_1.$

Podstawiając wartości otrzymujemy wynik końcowy:

$m_1 \approx 672 M_\odot,\qquad m_2 \approx 5,78\cdot 10^4 M_\odot.$

Zadanie pochodzi z Olimpijskiej Ligi Astronomicznej. Więcej informacji o konkursie i o obecnej edycji można znaleźć na stronie: https://almukantarat.pl/liga-astronomiczna/.

Korekta – Zofia Lamęcka

Treść

Rozwiązanie

II Olimpijska Liga Astronomiczna: Zadanie 3 z 5 serii

II Olimpijska Liga Astronomiczna: Zadanie 5 z 6 serii

II Olimpijska Liga Astronomiczna: Zadanie 1 z 4 serii

II Olimpijska Liga Astronomiczna: Zadanie 1 z 1 serii