W poprzednim artykule dowiedzieliśmy się jak obliczać współrzędne gwiazd na podstawie innych współrzędnych. Co innego jednak musimy wziąć pod uwagę? Jakie błędy uwzględnić przy pomiarach? Skąd wiedzieć, czy daną gwiazdę będzie można obserwować na naszej szerokości geograficznej?
Refrakcja atmosferyczna
Choć możemy mierzyć współrzędne gwiazd najdokładniejszymi metodami, prowadząc badania z powierzchni Ziemi, jesteśmy skazani na niedokładność. Przyczyną tego błędu jest obecność atmosfery. Choć na lekcjach fizyki można było potraktować powietrze jak próżnię, tutaj ma ono znaczenie.
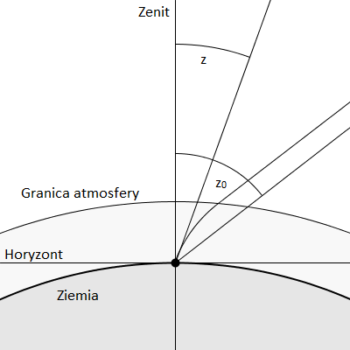
Światło podczas przechodzenia przez ośrodki o różnym współczynniku załamania światła ulega załamaniu. Przez to zjawisko, nasz obraz nieba jest zniekształcony. W zasadzie tylko zenit pozostaje wolny od zniekształcenia, gdyż jest pod kątem prostym do powierzchni Ziemi. Nasza planeta nie jest jednak idealną kulą, a powietrze nad nami się przemieszcza, powodując zniekształcenia.
Patrząc na rysunek powyżej, przedstawiający załamanie światła możemy zauważyć, że obserwowane przez nas obiekty będą miały zwiększoną wysokość , a odległość zenitalna zmaleje
. Kątem refrakcji będziemy nazywać kąt
.
Podzielmy atmosferę na równoległe warstwy o skokowo różnej gęstości, rosnącej w stronę Ziemi. Dla pierwszej warstwy zachodzi:
Dla każdej innej warstwy zachodzi analogiczny stosunek. Przekształcając go do postaci ilorazu mamy:
Pozwala to wyciągnąć wniosek, że . Wiemy, że
, bo jest to warstwa próżni. Mając przekształconą definicję refrakcji
, możemy obłożyć równanie sinusem:
Refrakcja jest małym kątem, więc oraz
, co daje nam
. Przekształcając mamy:
Oczywiście dane przybliżenia mają sens, gdy używamy radianów, nie stopni. Dla powietrza o ciśnieniu atmosferycznym i temperaturze
współczynnik załamania światła wynosi
. Po przejściu na sekundy kątowe otrzymujemy:
Wzór ten jest jedynie przybliżeniem i sprawdza się tylko dla pewnych odległości zenitalnych. Dla wzór ten dość dobrze opisuje rzeczywistość. Refrakcja mierzona na horyzoncie wynosi
, a według wzoru byłaby nieskończenie wielka. Dla dokładniejszych wyników warto zajrzeć do tablic. Wartość refrakcji zależy też od innych czynników, m.in. od temperatury powietrza, ciśnienia atmosferycznego, czy nawet wilgotności powietrza.
Przejście obiektów przez lokalny południk
Jednym ze specjalnych miejsc na naszym niebie jest lokalny południk. Ma on tę właściwość, że każda gwiazd musi w trakcie doby przeciąć go dwa razy. Gwiazdy najwyżej na niebie będą w momencie przekraczania południka lokalnego w części zawierającej zenit. Będzie to na łuku . Ponadto wszystkie będą się przemieszczały po liniach równoległych do
.
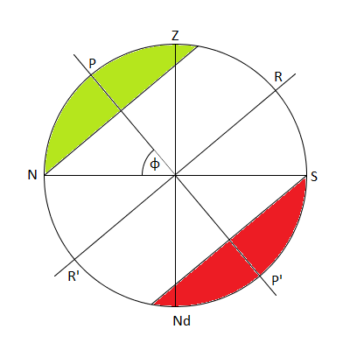
Przekrój obserwowanego nieba dla obserwatora z półkuli północnej (50°N). Oznaczenia: Z to zenit, Nd to nadir, R i R’ – miejsca przecięcia południka z równikiem niebieskim, P i P’ – północny i południowy biegun niebieski. Jest to perspektywa horyzontalna.
Te momenty będziemy nazywać kulminacjami, górnymi i dolnymi, bądź w skrócie górowaniami i dołowaniami. Wszystkie górowania mają miejsce na półokręgu , a dołowania na
. Dodatkowo podzielimy je na północne i południowe. Kulminacja będzie północna, jeśli gwiazda przechodzi przez punkt leżący na łuku
, południowa w przeciwnym wypadku. Możemy zatem wyróżnić 4 sytuacje. Są to: górowanie północne, górowanie południowe, dołowanie północne, dołowanie południowe. I tak wysokości danych kulminacji będziemy mogli opisać wzorami:
Górowanie północne: . Zachodzi dla gwiazd, gdzie
.
Górowanie południowe: . Zachodzi dla gwiazd, gdzie
.
Dołowanie północne: . Zachodzi dla gwiazd, gdzie
.
Dołowanie południowe: . Zachodzi dla gwiazd, gdzie
.
Gwiazdy okołobiegunowe oraz wschodzące i zachodzące
Widzimy już, jak wielkie znaczenia ma nasza szerokość geograficzna. Przemieszczenie się na Ziemi wzdłuż południka robi sporą różnicę z astronomicznego punktu widzenia. Zmiana położenia wzdłuż równoleżnika zmieni tylko czasy wschodów i zachodów gwiazd. Zmiana szerokości geograficznej pociąga za sobą obszar nieba, który jesteśmy w stanie zobaczyć. Gwiazdy można podzielić na dwie kategorie. Gwiazdy okołobiegunowe, które są zawsze nad/pod horyzontem, oraz gwiazdy wschodzące i zachodzące, czyli takie, których wysokość będzie zmieniać znak w trakcie doby.
Dla półkuli północnej:
Gwiazdą nigdy nie zachodzącą będzie taka, dla której .
Gwiazdą nigdy nie wschodzącą, będzie taka, dla której .
Gwiazdy należące do wschodzących i zachodzących będą te, które zaprzeczają poprzednim warunkom tj. .
Dla półkuli południowej:
Gwiazdą nigdy nie zachodzącą będzie taka, dla której .
Gwiazdą nigdy nie wschodzącą, będzie taka, dla której .
Gwiazdy należące do wschodzących i zachodzących będą te, dla których tj. .
Na biegunach Ziemi sprawa jest specyficzna. Z bieguna północnego można w zasadzie ujrzeć tylko gwiazdy o deklinacji dodatniej. Na dodatek nigdy nie będą one wschodzić, ani zachodzić. Podobnie jest na biegunie południowym, natomiast na równiku jest odwrotnie. Nie ma gwiazd, które stale są na niebie. Wszystkie wschodzą i zachodzą. Na dodatek każda z nich będzie widnieć na niebie pół doby (o ile nie przyćmi ich Słońce). Na to, czy jesteśmy daną gwiazdę zobaczyć w danym czasie, mają wpływ jeszcze inne zjawiska.
Rok, zodiak, gwiazdozbiory
Jednym z czynników, od którego może zależeć widoczność gwiazd, jest położenie Ziemi względem Słońca. Nawet jeśli obliczyliśmy, że dana gwiazda jest w zakresie zależnym od naszej szerokości geograficznej, może się okazać, że w danym dniu, musielibyśmy ją obserwować w dzień. Z uwagi na wielką jasność Słońca jest to niewykonalne. Z tego powodu możemy podzielić gwiazdozbiory (czyli obszary nieba) według pór roku. Nie znaczy to, że latem na pewno nie zobaczymy np. Oriona, ale będzie można go zobaczyć tylko wcześnie rano, gdy zaczyna się robić jasno, co utrudnia obserwacji.
Inną sprawą, na którą wpływ ma ruch roczny Ziemi i odchylenie osi obrotu od płaszczyzny ekliptyki, jest fakt, że Słońce i planety układu słonecznego nie poruszają się po równiku niebieskim, a raczej po ekliptyce — płaszczyźnie obrotu Ziemi wokół Słońca. Pas nieba wokół tego obszaru nazywamy zodiakiem. Nie jest on jednak równoznaczny z astrologicznym zodiakiem. Na naszym zodiaku znajduje się obecnie 13 gwiazdozbiorów, Słońce nie wchodzi w kolejne gwiazdozbiory dokładnie co miesiąc, a każdy z tych obszarów nie jest równy. Dodatkowo wskutek precesji, zmieniają się dni, w których w dany gwiazdozbiór wchodzi Słońce. Najlepszym tego przykładem jest fakt, że punkt Barana (punkt, w którym można obserwować Słońce podczas przesilenia wiosennego) obecnie znajduje się w gwiazdozbiorze Ryb, a za około 500 lat będzie wkraczał do gwiazdozbioru Wodnika. W Baranie znajdował się w czasach starożytnych. Wtedy właśnie podzielono niebo na 12 równych części. Podział ten jest jednak umowny i wskutek precesji przesuwa się na naszym niebie.
Zadania
- Na jakich szerokościach geograficznych można obserwować Wegę (
Lyr)? Dla jakich szerokości jest ona gwiazdą nie zachodzącą?
- Na jakiej wysokości góruje i dołuje Wega w Krakowie?
Dane do zadań
Wega:
Kraków:
Rozwiązania
Zadanie 1
Wega jest gwiazdą o deklinacji dodatniej, więc na pewno będzie widoczna z północnej półkuli. Pozostaje nam ustalić, gdzie na półkuli południowej staje się gwiazdą nie wschodzącą. Stosując wzór na gwiazdy nigdy nie wschodzące otrzymujemy . Ostatecznie
. Zaś na półkuli północnej będzie nigdy nie zachodzącą gdy
. Dostajemy więc
.
Zadanie 2
Zgodnie z podanymi wzorami Wega będzie górować po stronie południowej na wysokości , a dołować na wysokości
.
- Astronomia w Geografii, J. Mietelski