Treść
Kometa C/2023 P1 (Nishimura), która 12 września dokonała przelotu najbliżej Ziemi, odkryto 11 sierpnia 2023 roku. Jej współrzędne w układzie ekliptycznym wynosiły wtedy
,
,
prędkość radialna ,
prędkość styczna w długości ekliptycznej ,
w szerokości ekliptycznej ,
odległość od Ziemi .
Wyznacz odległość kątową komety od Słońca w momencie jej peryhelium z punktu widzenia obserwatora umieszczonego w środku Ziemi.
Załóż kołowość orbity Ziemi, pomiń wpływ ciał innych niż Słońce na ruch komety. Dane o pozycji Słońca w każdym dniu roku możesz znaleźć w Roczniku Astronomicznym bądź innych dostępnych w internecie źródłach.
Autor: Aleksander Łyczek
Rozwiązanie
 Aleksander Łyczek
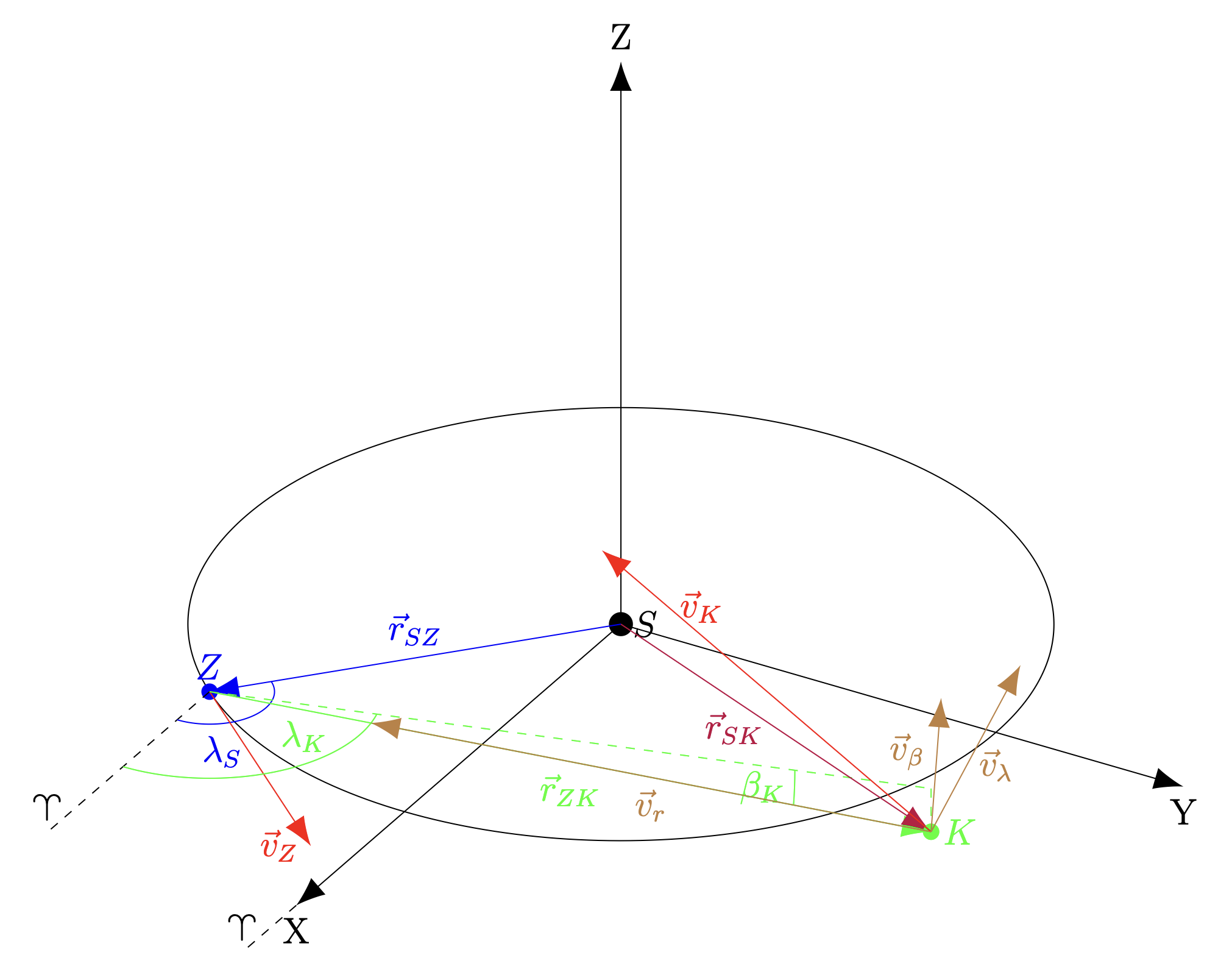
Aleksander ŁyczekRozwiązanie z reguły najlepiej zacząć od dobrego rysunku rozważanej sytuacji, takiego chociażby jak ten powyżej. Następnie należy się zastanowić, co musimy wzynaczyć po drodze, by dojść do rozwiązania problemu. W zadaniu należy policzyć elongację komety w momencie jej przejścia przez peryhelium. Aby to zrobić, niezbędne jest określenie położenia punktu peryhelium w przestrzeni, jak również położenia Ziemi w tejże chwili czasu. Peryhelium możemy określić dzięki znajomości wektorów położenia i prędkości komety w pewnej chwili czasu, gdyż wektory te wyznaczają płaszczyznę ruchu komety, jak również pozwalają określić rozmiar orbity, po której okrąża ona Słońce. Następnie dzięki określeniu odległości kątowej między peryhelium a aktualnym położeniem będzie można z II prawa Keplera wyznaczyć czas, po którym to przejście nastąpi. Mając ten czas, można łatwo policzyć wektor położenia Ziemi w momencie przejścia komety przez peryhelium i tym samym szukaną elongację mniejszego ciała.
Rozwiązanie zaczniemy od wprowadzenia kartezjańskiego układu współrzędnych, początek znajduje się w Słońcu, oś X wskazuje na punkt Barana, zaś oś Z na północny biegun ekliptyczny — wtedy płaszczyzna XY pokrywa się z płaszczyzną orbity Ziemi wokół Słońca. Bazując na rysunku, chcemy wyznaczyć wektory oraz
.
Zacznijmy od znalezienia wektora położenia komety. Na podstawie rysunku można zauważyć, że wektor jest sumą wektorów
oraz
. Wektor
ma znaną długość równą 1 AU, leży w płaszczyźnie ekliptyki oraz tworzy z osią X kąt
(
w dniu 11 sierpnia 2023 w południe czasu polskiego), zatem jego współrzędne w układzie kartezjańskim wynoszą
Położenie komety względem ziemi jest natomiast określone w sferycznym układzie współrzędnych poprzez wielkości ,
oraz
. Przejście z układu sferycznego na kartezjański odbywa się następująco:
Wektor wynosi zatem
Długość wektora wyznaczamy z twierdzenia Pitagorasa.
Wyznaczenie jest nieco bardziej problematyczne, gdyż w zadaniu mamy podane niebezpośrednio aż trzy niezależne informacje o ruchu komety względem Ziemi, mianowicie o prędkościach oznaczonych na rysunku
,
oraz
, których składowe należy wyznaczyć w układzie kartezjańskim i dodać do siebie, by dostać wektor prędkości komety względem Ziemi
. Ostatni wektor jest niczym innym jak różnicą wektorów
i
, co implikuje, że
. Poniżej znajdują się rozpisane wszystkie niezbędne nam wektory prędkości, ewentualny dowód tego, że mają one właśnie taką postać, pozostawiam Czytelnikowi. Wartość prędkości Ziemi w ruchu Słońca można wyznaczyć ze wzoru na ruch po okręgu albo znaleźć w internecie,
.
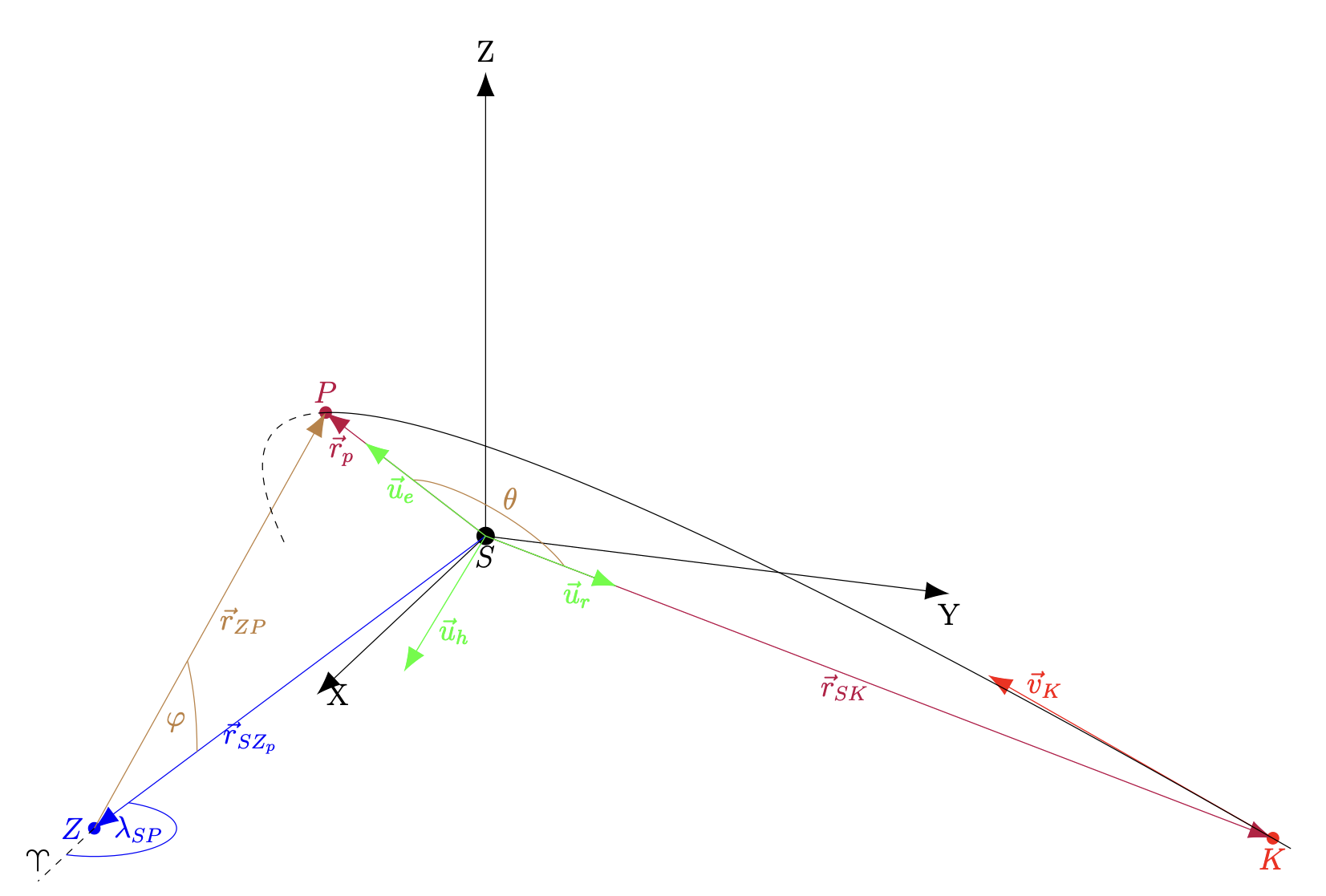
Zanim przejdziemy do dalszych obliczeń, warto wykonać rysunek obrazujący ewolucję sytuacji. Na obrazku poniżej czarna krzywa przedstawia trajektorię, którą kometa pokonuje do osiągnięcia peryhelium, — jej anomalia prawdziwa w chwili początkowej,
— punkt peryhelium,
— szukana elongacja,
— długość ekliptyczna Słońca w momencie przejścia komety przez peryhelium.
 Aleksander Łyczek
Aleksander ŁyczekZnając położenie i prędkość komety względem Słońca, można policzyć jej całkowitą energię mechaniczną oraz moment pędu na jednostkę masy, oznaczony dalej jako Z zasady zachowania energii mamy
Moment pędu jest zdefiniowany jako iloczyn wektorowy wektorów położenia i prędkości, zatem
Z momentu pędu można wyznaczyć mimośród orbity komety, gdyż obowiązuje zależność
Mamy wielką półoś, mamy mimośród, możemy zatem wyznaczyć odległość komety od Słońca w peryhelium:
Nadal potrzebujemy jednak wektora określającego położenie przestrzenne peryhelium, jak również czasu do przejścia komety przez nie. Do wyznaczenia pierwszej z tych rzeczy można użyć gotowej formuły (hasło wyszukiwania w Google: “eccentricity vector”), albo zauważyć, że wektor ten leży w płaszczyźnie orbity, zatem jest prostopadły do wektora momentu pędu komety, jak również tworzy z wektorem położenia komety kąt równy anomalii prawdziwej, do znalezienia której dysponujemy potrzebnymi danymi. Oznaczmy ten wektor wskazujący od Słońca do peryhelium orbity przez i załóżmy, że ma on długość 1, wtedy
. Dodatkowo wprowadźmy jednostkowe wektory
oraz
, skierowane odpowiednio wzdłuż wektorów
oraz
.
Z własności iloczynu skalarnego wektorów wiemy, że . Ponadto zauważmy, że wektory
i
leżą w płaszczyźnie orbity, zatem wektor będący wynikiem ich iloczynu wektorowego jest do niej prostopadły, a tym samym równoległy do wektora
. Ponadto długość wektora
z własności iloczynu wektorowego wynosi
, z czego możemy wywnioskować, że
. Razem z równaniem na iloczyn skalarny daje to układ 4 równań do rozwiązania:
Mogłoby się wydawać, że mamy aż 4 równania, a tylko 3 niewiadome, więc otrzymany układ równań jest sprzeczny, jednak pierwsze 3 równania wynikające z iloczynu wektorowego są liniowo zależne, tzn. dowolne z nich można przedstawić jako kombinację liniową dwóch pozostałych. Niezależne równania są de facto 3, a ich rozwiązanie wygląda następująco (dowód pozostawiam Czytelnikowi):
Anomalię prawdziwą obliczamy z równania elipsy w układzie biegunowym o środku w jej ognisku:
Możemy teraz podstawić wyliczoną wartość do wzorów na składowe wektora
i wyznaczyć położenie peryhelium w przestrzeni. Zostaje zatem ostatni akcent, czyli wyznaczenie czasu do przejścia komety przez peryhelium. Można w tym celu skorzystać z II prawa Keplera, wyznaczając uprzednio pole wycinka elipsy o kącie
i środku w jej ognisku (da się to zrobić bez całkowania, jeśli zauważy się fakt, że elipsa to okrąg o promieniu
spłaszczony w jednej osi o czynnik
). My jednak w tym celu posłużymy się związkami jakie zachodzą między anomaliami: prawdziwą
, mimośrodową
oraz średnią
. Związki te są bezpośrednią konsekwencją II prawa Keplera oraz relacji geometrycznych między elipsą a opisanym na niej okręgiem. Anomalię średnią definuje się jako
, gdzie
to okres obiegu ciała niebieskiego, zaś
odstęp czasu między chwilą obecną a momentem przejścia przez peryhelium. Anomalię średnią z mimośrodową wiąże tzw. równanie Keplera (wartości kątów muszą być podane w radianach):
Z kolei anomalia mimośrodowa jest powiązana z prawdziwą następującą relacją
Następnie wyznaczone podstawiamy równania Keplera, by otrzymać wartość anomalii średniej. Do wyznaczenia
potrzeba nam zatem jeszcze okresu obiegu komety wokół Słońca, który obliczamy z III prawa Keplera:
Ponieważ założyliśmy, że orbita Ziemi jest kołowa, w momencie przejścia komety przez peryhelium, długość ekliptyczna Słońca będzie wynosić
Wektor położenia Ziemi względem Słońca w tej chwili wynosi więc
Relacja pomiędzy wektorami, z której możemy wyznaczyć położenie komety w peryhelium względem Ziemi, wygląda podobnie jak na początku rozwiązania. Wtedy zachodziła relacja , natomiast teraz mamy
Kąt elongacji jest kątem pomiędzy wektorem
oraz wektorem przeciwnym do wektora
, czyli
. Oba wektory znamy, zatem kąt
można wyliczyć np. z własności iloczynu skalarnego.
