W poprzednim artykule poruszyliśmy temat gwiazd zmiennych. W tym postaram się przybliżyć czytelnikom jeden szczególny typ gwiazd zmiennych, mianowicie gwiazdy układów zaćmieniowych. Wspomnę też o nieco o masie Eddingtona oraz pewnym przybliżeniu, które dostarczy nam ważnych informacji o gwiazdach.

Układy zaćmieniowe

Przede wszystkim musimy sobie powiedzieć, czym są gwiazdy zaćmieniowe. Gwiazdy zaćmieniowe to takie gwiazdy, które występują w układach co najmniej podwójnych. Ponadto płaszczyzna ich orbit musi być zbliżona do równoległej z kierunkiem obserwatora. Krótko mówiąc, gwiazdy podczas swojego ruchu orbitalnego muszą się zasłonić, choćby częściowo. Zjawisko jest analogiczne do zaćmienia Księżyca czy Słońca. W dalszych rozważaniach posłuży nam do analizy wykres nazywany krzywą jasności. To zwykła zależność jasności układu od czasu.

Klasyfikacja układów zaćmieniowych

Jako pierwszą klasyfikację omówimy tę polegającą na ocenie krzywej jasności. Wyróżnia się typy:

• EA (zmienne typu Algol) – w ich krzywej jasności zazwyczaj łatwo wykryć momenty kontaktu, między zaćmieniami jasność jest raczej na stałym poziomie. Zazwyczaj są to układy rozdzielone lub półrozdzielone.
  NightSkyInfo

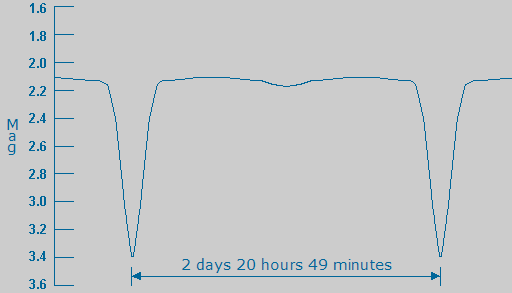
  Krzywa jasności Algola, przedstawiciela gwiazd zaćmieniowych typu EA.

• EB (zmienne typu Lyrae) – w tym przypadku obserwowane minima zazwyczaj nie są równej wielkości, a momenty kontaktu są trudniejsze do uchwycenia. Może to wynikać ze zdeformowanego kształtu tych gwiazd, miejscowych zmian jasności. Takie gwiazdy są już ze sobą w kontakcie, a ich deformacje są spowodowane siłami pływowymi.
  Van Hamme, Wilson and Guinan

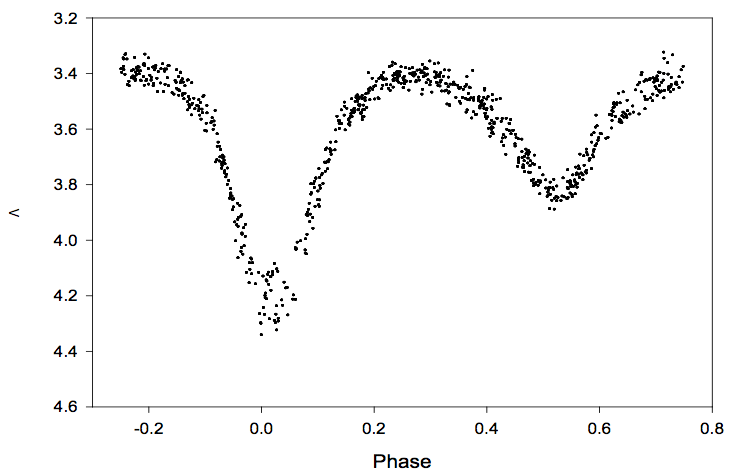
  Wykres gwiazdy Lyr, przedstawiciela gwiazd zaćmieniowych typu EB.

• EW (zmienne typu W UMa) – w tych przypadkach gwiazdy są już najpewniej w kontakcie. Krzywe blasku są zbliżone wyglądem do tych typu EB, jednak nie da się tutaj wyróżnić momentów kontaktu. Krzywa jest ciągle zmienna.
  Kerri Malatesta z AAVSO

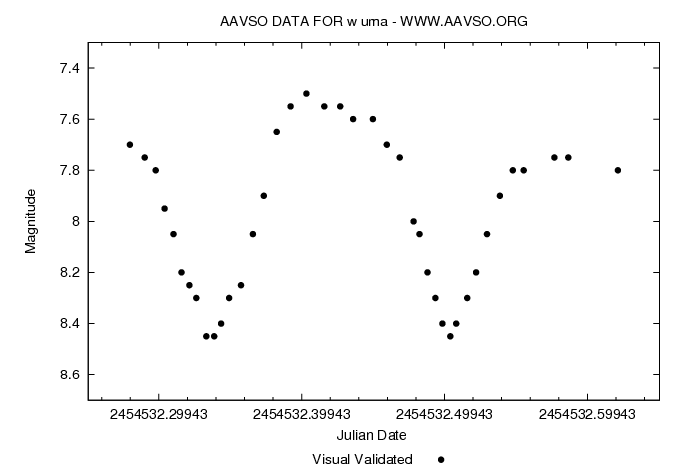
  Krzywa jasności gwiazdy W UMa, przedstawiciela gwiazd zaćmieniowych typu EW.

Innym możliwym podziałem układów zaćmieniowych jest klasyfikacja według wypełnienia powierzchni Roche’a, czyli powierzchni, na której potencjał wynikający z grawitacji oraz ruchu obrotowego jest równy zero.

• Układ rozdzielony — każdy ze składników leży wewnątrz powierzchni Roche’a. Gwiazdy na ogół mają oddzielną ewolucję. Mogą zmienić swój typ na układ półrozdzielony lub kontaktowy.
• Układ półrozdzielony — jeden ze składników wypełnia swoją powierzchnię Roche’a. Przez punkt Lagrange’a L1 wypływa materia z gwiazdy zazwyczaj lżejszej i większej do cięższej i mniejszej.
• Układ kontaktowy — oba składniki wypełniają powierzchnię Roche’a. Gwiazdy mają wspólną powierzchnię i warstwę konwekcyjną.

Powyższy podział można jeszcze dalej dzielić w zależności od typów gwiazd należących do układu.

Analiza krzywej blasku

Krzywe blasku mają różne kształty, jednak niemal zawsze sprawdza się dla nich poniższy schemat.

Mohammad El-Mahameed, edycja: Michał Stefanik

Z powyższego obrazka będą nas interesowały zaznaczone punkty 1-4 oraz punkty przejściowe. W chwilach 1 oraz 3 gwiazdy nie stoją sobie na drodze, tak więc ich jasność jest ich łączną jasnością. W chwili 2 mniejsza gwiazda zostaje przysłonięta przez większą, zaś w momencie 4 mniejsza gwiazda przesuwa się przed większą.

Po pierwsze, znając czas między kolejnymi zdarzeniami n.p. kolejnymi momentami a), jesteśmy w stanie znaleźć okres orbitalny układu. Czasem jednak na takim wykresie na osi nie podaje się czasu, a fazę.

Z takiego wykresu można przede wszystkim odczytać jasność obu gwiazd razem oraz większej gwiazdy (jeśli przysłania całkowicie mniejszą). Na ich podstawie da się znaleźć jasność mniejszej z gwiazd. Wychodząc od prawa Pogsona:

(1)  

Po paru przekształceniach dostajemy:

(2)  

Znając dodatkowo jasność Słońca, a tę można znaleźć w tablicach, możemy wyrazić strumień naszych gwiazd w stosunku do strumienia Słońca.

(3)  

Analogicznie postępujemy dla drugiej gwiazdy.

Jeśli znamy dodatkowo odległość takiego układu od Ziemi lub ogólnie Układu Słonecznego, możemy pokusić się o obliczenie ich jasności absolutnych , , czy mocy promieniowania , . Odległość takiego układu można znaleźć przy użyciu paralaksy słonecznej.

Jasność a masa

Czy istnieje prosty wzór, który łączyłby jasność gwiazdy z jej masą? Nie. Natomiast z rozważań teoretycznych Arthur Eddington wyprowadził wzór znany jako jasność Eddingtona. Równanie zostało wyprowadzone na podstawie faktu, że na granicy gwiazdy musi zostać zachowana równowaga sił grawitacji oraz ciśnienia promieniowania. Nie uwzględnia on wszystkich zjawisk, które będą wzięte pod uwagę w innych dokładniejszych wzorach.

(4)  

Jest to z grubsza pewne ograniczenie na jasność przy danej masie. Oprócz tego mamy pewien wzór wynikający bardziej z obserwacji:

(5)  

Dla części gwiazd z ciągu głównego () wzór jest prawdziwy dla oraz . Często również przybliża się wartość , która lepiej sprawdza się dla mniejszych gwiazd. Nie jest to najdokładniejsze z przybliżeń, jednak w przypadku prostego szacowania powinno wystarczyć.