Dlaczego korzysta się z teleskopów do obserwacji nieba? Odpowiedź na to pytanie, jest trywialna: przez teleskop widać więcej niż gołym okiem. Ale co dokładnie sprawia, że teleskopy potrafią poprawić ograniczenia ludzkiego wzroku? Jakie parametry tego urządzenia sprawiają, że teleskop jest w stanie pokazać więcej niż nieuzbrojone oko?

Powiększenie i zdolność rozdzielcza

W pierwszej chwili, na myśl przychodzi powiększenie. Podobnie, jak wiele innych przyrządów optycznych teleskop powiększa obserwowany obraz. Aby obliczyć powiększenie teleskopu, należy podzielić ogniskową obiektywu przez ogniskową okularu.

Istnieją jednak pewne fizyczne ograniczenia, które ustanawiają górną granicę użytecznego powiększenia teleskopu. Najczęściej przyjmuje się, że maksymalne powiększenie teleskopu wynosi 2D, gdzie D jest średnicą obiektywu w milimetrach.

Dlaczego jednak powiększanie obrazu wydaje się tak ważne? Jedną z istotnych cech układów optycznych, która utrudnia precyzyjne obserwacje, jest zdolność rozdzielcza. Zdolność rozdzielczą definiuje się, jako najmniejszą odległość kątową pomiędzy dwoma punktami, przy której można te punkty rozróżnić. Przy mniejszej odległości punkty zleją się ze sobą. Przyczyną zlewania się blisko położonych punktów jest dyfrakcja światła na szczelinach.

Zdolność rozdzielcza dla ludzkiego oko wynosi ok. 3 minut kątowych (3’), lecz niektórzy ludzie mogą dostrzegać nawet większe szczegóły. Wartość ta oznacza, że człowiek patrzący na dwa źródła światła oddalone od siebie o 1 metr, z odległości nieco większej niż kilometr, zobaczy je jako pojedynczą plamę.
Aby obliczyć zdolność rozdzielczą teleskopu, można skorzystać z tzw. kryterium Rayleigha. Wynika z niego wzór na zdolność rozdzielczą w radianach:

Gdzie λ jest długością fali, którą odbiera teleskop (maksimum czułości ludzkiego oka przypada dla ok. 550 [nm]), a d_ob oznacza średnicę obiektywu. Należy pamiętać, że podany powyżej wzór dotyczy przypadku granicznego. Przykładowo, jeżeli źródła światła mają różną jasność, potrzeba lepszej zdolności rozdzielczej, aby je rozróżnić.

Znając odległość kątową między punktami, można obliczyć powiększenie potrzebne do ich rozróżnienia. Jest ono równe stosunkowi zdolności rozdzielczej oka, do odległości kątowej pomiędzy tymi punktami.

Światłosiła i wady optyczne

Galaktyka w Andromedzie (M31) w najszerszym miejscu ma szerokość kątową niecałych 3°, to tyle, co szerokość złotówki trzymanej na wyciągniętej ręce. M31 jest więc na tyle duża, że ani powiększenie, ani zdolność rozdzielcza nie mają kluczowej roli w jej obserwacji. Jednakże M31 jest ledwie widoczna gołym okiem, a przez teleskop sprawia oszałamiające wrażenie. Trzecim parametrem pozwalającym teleskopom na pokazywanie nam więcej jest światłosiła.

Światłosiłę można określić, jako zdolność do zbierania światła przez teleskop. Określa się ją, jako stosunek średnicy obiektywu do jego ogniskowej.

Oprócz ograniczeń narzuconych przez zdolność rozdzielczą oraz światłosiłę istnieją też inne problemy, które mogą utrudniać obserwacje. Są nimi między innymi wady optyczne soczewek.

Jedną z tych wad jest aberracja sferyczna. Dotyczy ona soczewek oraz zwierciadeł sferycznych. Polega ona na rozmyciu ogniska soczewki, dla promieni oddalonych od osi optycznej. Wynika ona z przybliżeń stosowanych w optyce geometrycznej. Widzianym efektem tej aberracji jest rozmywanie się obrazu na krawędziach, tym większe im dalej od środka. Ten typ aberracji jest tym bardziej zauważalny, im większą światłosiłę ma teleskop. Korygowanie tej wady polega na stosowaniu zwierciadeł innych niż sferyczne.

Inną wadą dotyczącą już jedynie soczewek, jest aberracja chromatyczna. Wynika ona z dyspersji światła, czyli zależności jego prędkości w danym materiale od długości. Z powodu dyspersji, współczynniki załamania światła nie są takie same dla różnych zakresów światła. Na skutek tego ognisko soczewki dla światła czerwonego może być w innym miejscu niż dla światła niebieskiego, co wywołuje barwne rozmycie kształtów na brzegach obrazu. Do korygowania aberracji chromatycznej stosuje się specjalne układy soczewek wykonanych z różnych materiałów.

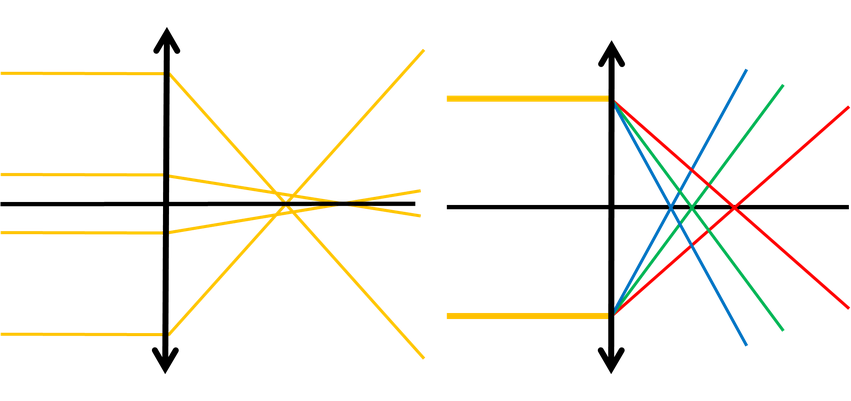Radosław Kubiś

Bieg promieni świetlnych na soczewki: obarczoną aberracją sferyczną (lewa grafika) i obarczoną aberracja chromatyczną (prawa grafika). Dla przejrzystości rysunku światło białe zostało zaznaczone na żółto.

Ostatnią poruszoną w tym artykule wadą optyczną jest koma (zwana również aberracją komatyczną). Polega ona na rozmyciu ogniska soczewki dla promieni padających pod kątem do osi optycznej. Soczewki posiadające komę tworzą obrazy w kształcie przecinka. Podobnie, jak w wypadku innych aberracji do korekcji komy stosuje się odpowiednie soczewki, lub ich zespoły. Obiektyw, lub układ optyczny wolny od komy oraz aberracji sferycznej nazywany jest aplanatem.

Zadania

• Teleskop o ogniskowej 1200 [mm] ma światłosiłę f/6. Jaka jest jego teoretyczna zdolność rozdzielcza dla światła widzialnego o długości λw = 500 [nm], a jaka dla podczerwieni o λp = 10 [μm]?
• Zwierciadło główne Kosmicznego Teleskopu Hubble’a ma średnicę 2,4 [m]. Oblicz teoretyczną zdolność rozdzielczą tego teleskopu. Struktury, o jakiej minimalnej wielkości w Mgławicy Kraba jest w stanie rozróżnić ten teleskop? Odległość Mgławicy Kraba od Ziemi wynosi 6300 lat świetlnych. W obliczeniach przyjmij długość fali świetlnej równą 500 [nm].
• Tzw. seeing to maksymalna zdolność rozdzielcza możliwa dla danych warunków atmosferycznych. Przy jakim seeingu możliwe byłoby zaobserwowanie góry Olympus Mons na powierzchni Marsa? Najmniejsza możliwa odległość pomiędzy Ziemią a Marsem wynosi 56 milionów [km]. Jak zmieni się wynik, jeżeli obliczenia wykonamy dla największej możliwej odległości: 401 milionów [km]? Średnica Olympus Mons wynosi w przybliżeniu 600 [km].

Zadanie 2 i 3 pochodzą z Astrolabium. Konkurs astronomiczny: Zdolność rozdzielcza. 2019

Rozwiązania zadań

Zadanie 1

Mając daną ogniskową oraz światłosiłę teleskopu, można wyznaczyć jego średnicę obiektywu.

Teraz, korzystając ze wzoru na zdolność rozdzielczą, można wyznaczyć jej wartości dla podanych w zadaniu długości fali.

Należy pamiętać, że podane wyżej wartości wynikają z czystej teorii i nie uwzględniają m.in. wpływu atmosfery.

Zadanie 2

Korzystając ze wzoru na zdolność rozdzielczość, należy wyznaczyć jej wartość dla teleskopu Hubble’a.

Teraz, za pomocą otrzymanej wielkości można obliczyć minimalną odległość między dwoma punktami Mgławicy Kraba x, które Teleskop Hubble’a jest w stanie rozróżnić. Z powodu bardzo małego kąta można pominąć funkcje trygonometryczne w obliczeniach (ważne, aby użyć wartości w radianach). Odległość Mgławicy Kraba od Ziemi została oznaczona, jako L.

Zadanie 3

Całe zadanie sprowadza się do pojedynczego wzoru. Należy obliczyć szerokość kątową Olympus Mons widzianego z Ziemi.

Najmniejszy seeing, jaki uzyskano na powierzchni Ziemi, wynosił ok. 0,5’’, więc teoretycznie można obserwować najwyższą górę Układu Słonecznego z powierzchni naszej planety.

Dla największej możliwej odległości między Ziemią a Marsem obliczenia wyglądają następująco:

Oznacza to, że dla tej odległości Olympus Mons staje się niewidoczny z powierzchni Ziemi nawet dla najlepszych teleskopów z powodu samego wpływu atmosfery.