Treść zadania 4 z 3 etapu XXXIX OA.
W ciasnych układach podwójnych materia przepływająca z jednej gwiazdy na drugą tworzy dysk akrecyjny. Materia ta, opadając ku gwieździe, wytraca swój moment pędu, wydzielając duże ilości energii. Większość tej energii zostaje wypromieniowana. Oceń temperaturę dysku w pobliżu powierzchni gwiazdy. Przyjmij, że masa gwiazdy, na którą opada materia, wynosi M = , jej promień to R = 10 km, a materia przepływa w tempie
. Masa Słońca wynosi M =
kg . Załóż, że materia opada ku gwieździe po ciasnej spirali.
Rozwiązanie
Zanim przejdziemy do rozwiązania, spróbujmy zastanowić się nad mechanizmem prowadzącym do powstawania dysków akrecyjnych oraz ogrzewania materii w nim się znajdującej. Kiedy materia zaczyna przepływać z drugiego obiektu do pierwszego na skutek silniejszego przyciągania grawitacyjnego przez masywniejszy obiekt, formuje strumień gazu zaczynający obiegać gwiazdę pierwszą po orbicie. W takim strumieniu dochodzi do zderzeń pomiędzy cząsteczkami gazu, które nie są idealnie sprężyste, zatem gaz ten stopniowo wytraca swoją prędkość, a tym samym energię kinetyczną, co skutkuje stopniowym zacieśnianiem orbity (mniejsza całkowita energia mechaniczna = niższa orbita). Rozproszona energia kinetyczna z kolei zmienia się przede wszystkim w energię wewnętrzną gazu, co skutkuje wzrostem jego temperatury.
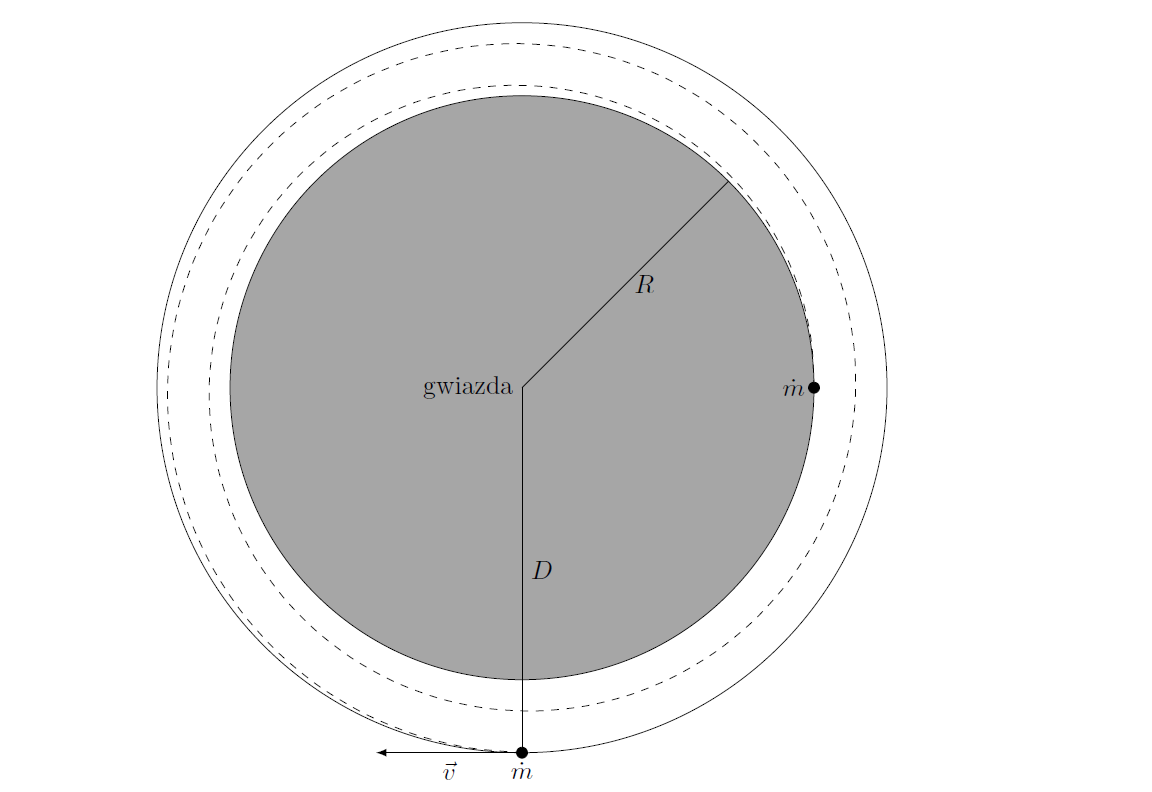
Zadanie wymaga od nas podania temperatury bardzo blisko powierzchni gwiazdy. Aby to zrobić, musimy podzielić cały dysk na małe, bardzo wąskie pierścienie i policzyć temperaturę tego najbliżej gwiazdy. Trafiamy tutaj na pewien problem. Jeżeli będziemy chcieli liczyć stratę energii przez materię oraz pole dla nieskończenie cienkiego pierścienia, w obydwu przypadkach dostaniemy 0. Chwilowo załóżmy, że materia spada na gwiazdę z orbity kołowej o promieniu D – kołowość orbity jest uzasadniona założeniem o opadaniu po bardzo ciasnej spirali – oraz że spadając, tworzy pierścień, którego temperatura jest wszędzie jednakowa. Sytuację w widoku z góry przedstawia Rysunek 1.
 Aleksander Łyczek
Aleksander ŁyczekRysunek 1: Schemat procesu opadania materii
Przez oznaczmy masę przepływającą przez pierścień w ciągu 1 sekundy (strumień masy):
=
=
=
.
Otrzymamy wtedy, że ilość wypromieniowanej energii przez materię na skutek zmiany promienia orbity kołowej z D na R wynosi, zgodnie ze wzorem na całkowitą energię mechaniczną w ruchu po orbicie kołowej
.
Ponieważ dzieje się to w czasie 1 sekundy, ta energia jest ilościowo równa mocy wydzielanej przez ten pierścień. Natomiast powierzchnia, na której wydziela się energia, jest równa:
(promieniuje zarówno z góry, jak i z dołu pierścienia). Używając wzoru na moc promieniowania ciała doskonale czarnego i podstawiając do niego P i S wyliczone wcześniej oraz rozwijając ze wzoru skróconego mnożenia
otrzymamy wzór na temperaturę:
,
w którym ani licznik, ani mianownik wyrażenia po prawej nie zeruje się dla D = R. Oznacza to, że temperatura naszego cienkiego pierścienia w odległości R wynosi:
.
Podstawiając wartości liczbowe, otrzymamy K, czyli wartość kilka tysięcy razy większą niż przeciętna temperatura powierzchni gwiazdy. Jest to wartość jednak jak najbardziej zgodna z rzeczywistością, gdyż dyski akrecyjne emitują większość energii w zakresie rentgenowskim, czyli zgodnie z prawem Wiena ich temperatury powinny mieścić się w zakresie od kilkuset tysięcy do kilkuset milionów kelwinów.
Prowadząc obliczenia, dokonano kilku uproszczeń, przede wszystkim założono całkowitą zamianę energii mechanicznej gazu w promieniowanie oraz brak przepływu energii wewnątrz dysku w inny sposób niż grawitacyjnie (brak wymiany ciepła między warstwami dysku), podczas gdy część energii może być nadal uwięziona w formie mechanicznej w postaci fal akustycznych poruszających się w gazie albo ruchów konwekcyjnych bądź poświęcana na jonizację gazu.
Rozwiązanie nadesłał Kamil Ciebiera.