Układy współrzędnych pozwalają nam na dokładne opisane położenia jakiegoś punktu. Na przykład w kartezjańskim układzie współrzędnych podanie współrzędnej x-owej pozwala na umiejscowienie punktu na prostej, dodanie y-owej opisuje punkt znajdujący się na płaszczyźnie, a dodanie trzeciego wymiaru i współrzędnej z-owej obejmuje już całą przestrzeń. Można zauważyć, że liczba współrzędnych potrzebna do dokładnego określenia punktu jest równa ilości wymiarów, w których ten punkt rozpatrujemy.
Artykuł napisała Lidia Lappo
Jeśli chodzi o układy sferyczne, pozwalają one nam na opisanie współrzędnych punktów na sferze. Powierzchnia sfery jest dwuwymiarowa, więc będziemy potrzebowali dwóch współrzędnych – użyjemy do tego dwóch kątów.
Układ współrzędnych geograficznych
Znany nam wszystkim z lekcji geografii układ współrzędnych geograficznych jest niczym innym jak układem współrzędnych sferycznych. Podając długość i szerokość geograficzną, jesteśmy w stanie określić położenie miast, gór czy Planetarium w Chorzowie (50.2906˚ N, 18.9920˚ E).
 Lidia Lappo
Lidia LappoDefinicja danych współrzędnych wygląda następująco:
Szerokość geograficzna (φ) to najmniejszy kąt pomiędzy płaszczyzną wyznaczoną przez równik a kierunkiem od środka układu określanym przez punkt.
Z definicji więc szerokość na równiku wynosi 0. Bieguny leżą na osi prostopadłej do płaszczyzny wyznaczonej przez równik. Współrzędna φ wynosi 90˚ (szerokości północnej N dla bieguna północnego i południowej S dla południowego). Widzimy, że zakres szerokości to [0˚ – 90˚].
Długość geograficzna (λ) to najmniejszy kąt między kierunkiem wyznaczanym przez dany punkt a płaszczyzną południka zerowego Greenwich.
Nie ma opartego na fizyce albo matematyce powodu, dla którego właśnie tam jest wyznaczony południk zerowy. Po prostu historycznie się tak złożyło, że jest tam, gdzie jest, czyli w Anglii, ale przechodzi też przez inne kraje.
Możemy zaznaczyć kilka punktów o tej samej szerokości. Nietrudno zauważyć, że punkty o tej samej szerokości tworzą coraz to mniejsze okręgi w miarę zbliżania się do biegunów. Takie okręgi o jednakowej szerokości geograficznej nazywamy równoleżnikami (bo wszystkie są do siebie równoległe). Największym równoleżnikiem jest oczywiście równik.
Południkiem jest linia na sferze łącząca wszystkie punkty o takiej samej długości geograficznej. Południki mają kształt półkola.
Mierzony na wchód kąt długość geograficzna stopniowo się zwiększa do 180˚, tak samo, gdy mierzymy w kierunku zachodnim. By uniknąć nieporozumień (w końcu istnieją dwa południki o długości 10˚) musimy precyzować, w jakim kierunku mierzyliśmy, czy długość jest zachodnia (W) czy wschodnia (E).
Na przykładzie siatki geograficznej widzimy, że żeby dobrze zdefiniować układ współrzędnych sferycznych, potrzebujemy dwóch punkty naprzeciwko siebie (biegunów) lub koła wielkiego (równik) oraz punkt początkowy (Greenwich).
Układ współrzędnych równikowych
Równonocny
Układ współrzędnych geograficznych jest niezwykle przydatny do określania położenia na Ziemi. Dla określenia położenia gwiazd używamy układu równikowego równonocnego. Gwiazdy ze względu na to, że są od nas oddalone i ich ruchy własne zwykle są pomijalne, mają stałe współrzędne w tak zdefiniowanym układzie (Vega ma współrzędne δ = 38° 47′ i α = 18h 36m).
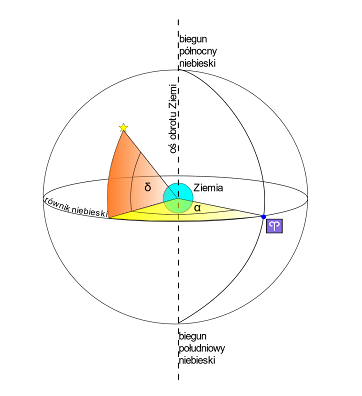
Siatkę definiujemy przy pomocy biegunów niebieskich. Leżą na przedłużeniu osi obrotu Ziemi i dlatego nie zmieniają położenia na niebie (Gwiazda Polarna znajdująca się na niebie w bardzo bliskiej okolicy północnego bieguna niebieskiego i obserwowana z tego samego miejsca na Ziemi będzie niezależnie od dnia i godziny znajdywała się w tym samym miejscu na niebie). Kołem wielkim będzie równik niebieski. Analogia między układem geograficznym jest dość oczywista. Naszym punktem początkowym jest punkt Barana, nazywany też punktem równonocy wiosennej, gdyż Słońce znajduje się w tym punkcie w czasie równonocy wiosennej. Punkt ten obecnie nie znajduje się już w gwiazdozbiorze Barana, lecz w gwiazdozbiorze Ryb, ze względu na precesję Ziemi.
 Lidia Lappo
Lidia LappoNajmniejszy kąt między płaszczyzną równika a kierunkiem wyznaczanym przez punkt (np. gwiazdą) nazywamy deklinacją δ. Deklinacja biegunów niebieskich północnego i południowego to odpowiednio 90° i -90° (różnicą między układem współrzędnych geograficznych jest wartość ujemna, która jest używana zamiast ciągłego precyzowania półkuli).
Kąt od kierunku wyznaczanego przez punkt Barana do kierunku naszej gwiazdy nazywamy rektascensją α. Zakres wartości rektascensji wynosi od 0° do 360°, z tym że zwykle te kąty podajemy w godzinach (od 0 do 24h – pełny obrót Ziemi, czyli 360°, zajmuje 24 godziny). Rektascensje liczymy na wschód od punktu równonocy wiosennej.
Pomijając wpływ precesji i wspomniane wcześniej ruchy własne gwiazd współrzędne równikowe równonocne, czyli deklinacja i rektascensja, są dla gwiazd stałe.
Godzinny
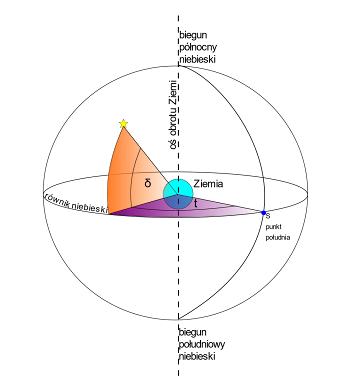
Dość podobnym nie tylko z nazwy układem współrzędnych jest układ równoleżnikowy godzinny. Jedną ze współrzędnych tego układu jest dokładnie tak samo zdefiniowana deklinacja δ. Za punkt początkowy służy przecięcie równika niebieskiego z południkiem lokalnym. Południkiem lokalnym nazywamy koło wielkie łączące bieguny niebieskie oraz zenit. Znajduje się ono na południu dla półkuli północnej i na północy dla południowej.
 Lidia Lappo
Lidia LappoKąt między kierunkiem wyznaczanym przez ten punkt a kierunkiem do np. gwiazdy to kąt godzinny t przyjmujący wartości od 0° do 360° lub od 0 do 24 h. Kąt mierzy się zgodnie z ruchem sfery niebieskiej, czyli na zachód. Kąt godzinny gwiazd zmienia się w ciągu doby (ponieważ Ziemia się obraca). Gdy ich kąt godzinny wynosi 0 h, gwiazdy górują (są najwyżej nad horyzontem), z kolei gdy wynosi 12 h, następuje dołowanie gwiazdy.
Wspomniane układy są bardzo uniwersalne: podane współrzędne nie zmieniają się niezależnie od pozycji obserwatora na Ziemi. Są jednak trudniejsze w użyciu, wymagają używania atlasów albo bardzo dobrej znajomości nieba.
Układ współrzędnych horyzontalnych
Lokalny układ współrzędnych, jakim jest układ horyzontalny, ułatwia komunikację między obserwatorami znajdującymi się w tym samym miejscu o tej samej porze. Można go używać zamiast uciążliwego pokazywania palcem – „Patrz tam! Jaka ładna gwiazdka”.
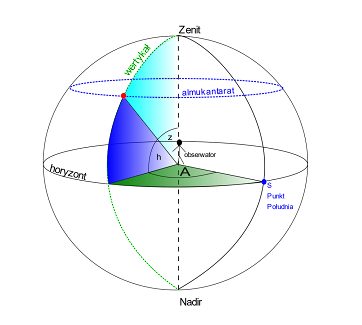
Naszym kołem wielkim jest horyzont. Biegunami układu są Zenit, czyli punkt pionowo nad nami na niebie, oraz niewidoczny Nadir, który jest dosłownie pod nami po drugiej stronie Ziemi. Punktem początkowym jest punkt kardynalny południa S. Koło wielkie przechodzące przez bieguny niebieskie, zenit, nadir i punkty kardynalne północy i południa nazywamy południkiem lokalnym.
 Lidia Lappo
Lidia LappoPierwszą współrzędną jest wysokość h (albo wysokość horyzontalna), czyli jak nie trudno się domyśleć kąt określający wysokość gwiazdy nad horyzontem. Przyjmuje wartości od -90° do 90°. Czasami zamiast wysokości podaje się odległość zenitalną, czyli kąt pomiędzy kierunkiem na gwiazdę a zenitem. Odległość zenitalna i wysokość horyzontalna dopełniają się do 90°. Punkty o tej samej wysokości nad horyzontem nazywamy almukantaratem.
Drugą współrzędną jest znany geografom azymut A, z tą różnicą, że geografowie liczą azymut od północy, astronomowie preferują definicję azymutu jako kąta pomiędzy południem a kierunkiem do obiektu (np. gwiazdy) mierzony w kierunku zachodnim. Zakres azymutu to oczywiście 0°-360°. Punkty o takim samym azymucie nazywamy wertykałem. Pierwszym wertykałem nazywane jest prostopadłe do południka lokalnego koło wielkie przecinające punkty kardynalne wschodu i zachodu oraz zenit i nadir.
Układ współrzędnych ekliptycznych
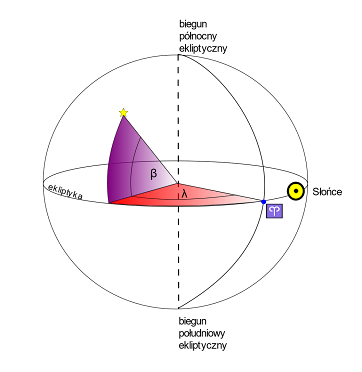
Podstawą tego układu jest ekliptyka, czyli roczna droga Słońca po sklepieniu niebieskim. Przy pomocy ekliptyki wyznaczamy bieguny ekliptyczne (dzięki osi prostopadłej do płaszczyzny ekliptyki). Punkt początkowy to wspomniany wcześniej punkt Barana (nie powinno dziwić, że znajduje się na ekliptyce, w końcu skoro Słońce pojawia się tam w czasie równonocy wiosennej, to punkt ten należy do rocznej drogi Słońca po sklepieniu niebieskim).
 Lidia Lappo
Lidia LappoKąt pomiędzy ekliptyką a kierunkiem do obiektu nazywamy szerokością ekliptyczną β w zakresie od -90° do 90°, analogicznie do poprzednio omówionych układów. Długością ekliptyczną λ nazywamy kąt między kierunkiem do obiektu a punktem Barana w zakresie od 0° do 360°.
Z definicji szerokość ekliptyczna Słońca zawsze jest równa zero. Ponieważ obiekty w Układzie Słonecznym poruszają się w mniej więcej tej samej płaszczyźnie, planety i Księżyc też będą widoczne w okolicy ekliptyki. Dlatego układ ten jest wygodny do opisywania ruchu ciał Układu Słonecznego.
Długość ekliptyczna Słońca zmienia się w ciągu roku. Znając długość ekliptyczną Słońca można wyznaczyć datę (bądź na odwrót przy pomocy daty – długość ekliptyczną). Dokładne dane można sprawdzić w katalogu. Jeśli chodzi o orientacyjne wartości, to wiemy, że w dniu równonocy wiosennej długość Słońca wynosi 0°, w czasie przesilenia letniego 90°, równonoc jesienna to odpowiednio 180° i 270° dla przesilenia zimowego.
Układ współrzędnych galaktycznych
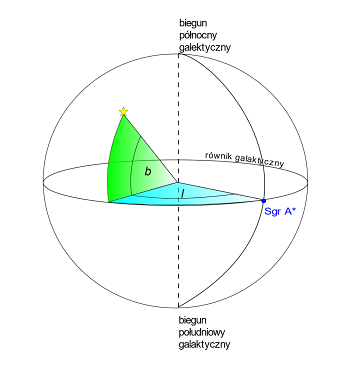
Tak samo jak układ ekliptyczny, układ współrzędnych galaktycznych definiujemy za pomocą koła wielkiego, które leży w płaszczyźnie galaktyki. To jest równik galaktyczny. Z jego pomocą definiowane są bieguny galaktyczne. Punktem początkowym jest radioźródło Sagittarius A* w centrum Drogi Mlecznej. Analogicznie do poprzedniego układu wykorzystujemy szerokość galaktyczną b (kąt od równika galaktycznego) i długość galaktyczną a (kąt mierzony od Sgr A* w tym samym kierunku, co rektascensję).
 Lidia Lappo
Lidia LappoPodsumowanie
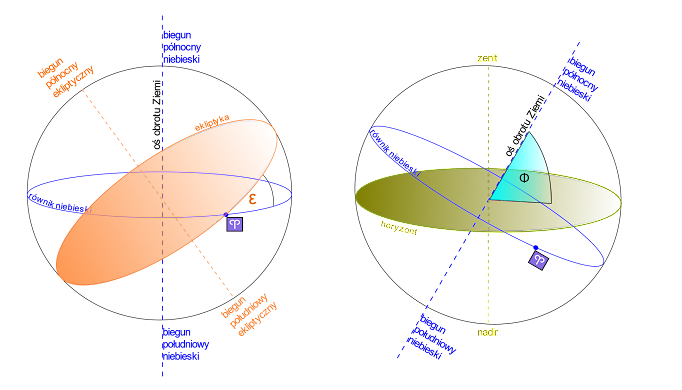
Biegłe używanie kilku układów współrzędnych i przechodzenia z jednego do drugiego wymaga praktyki. Na koniec porównanie dwóch układów względem siebie. Na pierwszym rysunku przedstawiono układ równikowy i układ ekliptyczny. Nachylenie tych układów względem siebie ε aktualnie wynosi 23°26,3´. Na drugim rysunku układ równikowy jest porównywany z układem ekliptycznym. Nachylenie tych dwóch układów względem siebie jest różne w zależności od szerokości geograficznej φ obserwatora w układzie horyzontalnym.
 Lidia Lappo
Lidia LappoPorównanie wszystkich układów współrzędnych
| Układ współrzędnych | Geograficzny | Równikowy Równonocny | Równikowy Godzinny | Horyzontalny | Ekliptyczny | Galaktyczny |
|---|---|---|---|---|---|---|
| Bieguny układu | Biegun północny i południowy | Biegun niebieski północny i południowy | Biegun niebieski północny i południowy | Zenit i nadir | Biegun ekliptyczny północny i południowy | Biegun galaktyczny północny i południowy |
| Koło Wielkie Układu | Równik | Równik niebieski | Równik niebieski | Horyzont | Ekliptyka | Koło Wielkie pokrywające się z płaszczyzną galaktyki |
| Punkt Początkowy | Południk zerowy Greenwich | Punkt Barana | Punkt przecięcia się równika niebieskiego i południka lokalnego | Punkt kardynalny południa | Punkt Barana | radioźródło Sagittarius A* |
| Współrzędne sferyczne | Szerokość i Długość geograficzna | Deklinacja i Rektascensja | Deklinacja i Kąt godzinny | Wysokość horyzontalna i Azymut | Szerokość i Długość ekliptyczna | Szerokość i Długość galaktyczna |




