Poruszając się po powierzchni niebieskiej planety określamy nasze położenie przy użyciu dwóch współrzędnych – szerokości oraz długości geograficznej. Jest to uniwersalny sposób by poinformować kogoś o tym, gdzie na Ziemi się znajdujemy. Zastanówmy się jednak nad tym, w jaki sposób przekazać komuś informację o położeniu pewnego obiektu na sferze niebieskiej. Zilustrujemy ten problem następującym przykładem: dwóch przyjaciół amatorów Franek i Stasiu prowadzą obserwacje ze swoich domów, które zlokalizowane są w dość odległych od siebie zakątkach świata. Franek dostrzegł przez swój teleskop pewien interesujący obiekt, którego współrzędne azymutalne odczytał z tego odpowiednio skalibrowanego przyrządu. Chciałby podzielić się ze Stasiem odkryciem, jednak współrzędne azymutalne na nic się zdadzą w tym wypadku, z racji tego że Stasiu znajduje się w innym miejscu i w dodatku korzysta z teleskopu na montażu paralaktycznym. Jak widać, posługiwanie się wieloma różnymi układami współrzędnych sferycznych, choć pozwala na dostosowanie używanego układu do konkretnych potrzeb, stawia nas przed problemem, by systematycznie zmieniać koordynaty z jednego układu na drugi.
Trójkąty paralaktyczne
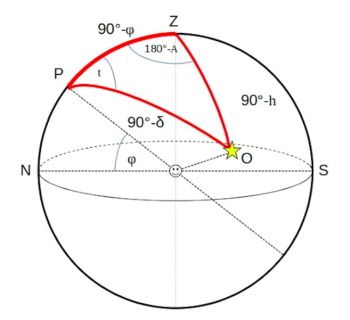
Dążąc do rozwiązania tego problemu, zacząć należy od skonstruowania pewnego szczególnego trójkąta sferycznego. Stawiając Franka w centrum naszych układów sferycznych, wybieramy trzy najważniejsze punkty – zenit, północny biegun niebieski oraz docelowy obiekt na niebie. Jak łatwo dostrzec, wszystkie boki tak zbudowanego trójkąta są fragmentami okręgów wielkich sfery. Trójkąt o takiej własności nazywamy paralaktycznym. Bok zawarty między zenitem a biegunem niebieskim należy do południka lokalnego i rozpina kąt będący dopełnieniem szerokości geograficznej do . Biegun niebieski oraz wybrany obiekt znajdują się na krawędzi koła godzinnego i spoglądając na nie w układzie współrzędnych równikowych, kąt wyznaczony przez te dwa punkty jest dopełnieniem deklinacji obiektu do
. Ostatnim bokiem trójkąta paralaktycznego jest fragment wertykału zawierającego obiekt, o mierze kątowej
w układzie horyzontalnym.
Po wyznaczeniu wszystkich trzech boków trójkąta paralaktycznego nadszedł czas, by przyjrzeć się kątom wewnętrznym. Kąt znajdujący się przy biegunie północnym jest kątem pomiędzy południkiem lokalnym a kołem godzinnym obiektu, co zgodnie z definicją wyznacza jego kąt godzinny . Odnosząc się ponownie do układu współrzędnych horyzontalnych można zauważyć, że kąt przy zenicie to dopełnienie azymutu obserwowanego ciała niebieskiego do kąta pełnego.
Wracając do wyjściowego problemu dwóch przyjaciół próbujących przekazać informację o położeniu tajemniczego obiektu, wykorzystamy wyżej wyznaczone kąty oraz boki trójkąta paralaktycznego do manewrowania pomiędzy różnymi zestawami współrzędnych.
Zamiana współrzędnych między układem horyzontalnym a równikowym
Załóżmy, że wyznaczone zostały współrzędne w układzie horyzontalnym czyli azymut oraz wysokość
i dodatkowo posiadamy informację na temat czasu gwiazdowego
dla miejsca obserwacji Franka oraz jego szerokość geograficzną
.
Korzystamy na początku z twierdzenia cosinusów dla trójkąta paralaktycznego
co po zastosowaniu wzorów redukcyjnych sprowadza się do następującej formy
w której jak widać, po prawej stronie równania występują jedynie znane nam wielkości, pozwalając w ten sposób wyznaczyć deklinację. Aby znaleźć kąt godzinny stosujemy twierdzenie sinusów, otrzymując ostatecznie równanie
Znamy już związek pomiędzy czasem gwiazdowym, kątem godzinnym oraz rektascensją wybranego punktu na niebie, który dany jest wzorem
co pozwala wyliczyć nam drugą współrzędną równikową równonocną. Udało nam się zatem otrzymać współrzędne, które Stasiu może wykorzystać do zlokalizowania obiektu na sferze niebieskiej. Naturalnie pojawia się jednak kolejne pytanie, a mianowicie czy metodę tę da się odwrócić, by ze współrzędnych równikowych równonocnych otrzymać horyzontalne na danej szerokości geograficznej o danym czasie gwiazdowym. Odpowiedź jest oczywiście twierdząca. W celu takiej zamiany zacząć należy od tego samego twierdzenia sinusów co uprzednio, w lekko przekształconej formie
w którym po prawej stronie brakuje nam informacji o wysokości. Zdobyć ją możemy, odwołując się ponownie do twierdzenia cosinusów
co po uproszczeniu przyjmuje postać
i pozwala na wyznaczenie , podstawienie obliczonej wartości do początkowego twierdzenia sinusów i ostatecznie wyznaczenie azymutu.
Wschód i zachód słońca
Wyżej omówiony algorytm transformowania współrzędnych między układami może być wykorzystany również do wyznaczenia związku pomiędzy azymutem wschodu lub zachodu słońca a jego deklinacją. W tym celu należy zauważyć jedynie, że wysokość w trakcie wschodu i zachodu wynosi zero, co po podstawieniu do użytego już wcześniej twierdzenia cosinusów daje następujące równanie
Azymut wschodu i zachodu jest zawsze symetryczny względem południka lokalnego, a zatem , z czego bezpośrednio wynika, że
.
Zamiana współrzędnych między układem ekliptycznym a równikowym
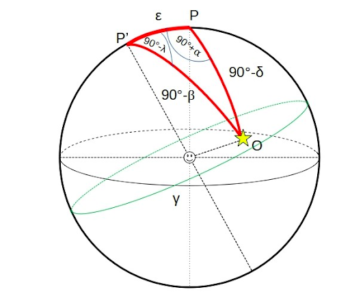
Wśród często używanych oraz pożytecznych układów sferycznych znajduje się także układ ekliptyczny. Aby zamienić jego współrzędne na współrzędne równikowe równonocne konieczne będzie skonstruowanie kolejnego trójkąta paralaktycznego o wierzchołkach w następujących punktach: północnym biegunie niebieskim (P), północnym biegunie ekliptycznym (P’) oraz wybranym obiekcie (O). W celu ustalenia formuł służących do transformowania współrzędnych konieczne jest ponownie określenie miar odpowiednich kątów oraz boków skonstruowanego trójkąta. Zaczynając od boku pomiędzy biegunami północnymi dostrzec można od razu, że jest to fragment okręgu wielkiego o mierze równej nachyleniu ekliptyki względem równika niebieskiego. Drugi bok prowadzący od bieguna ekliptycznego do obiektu O jest dopełnieniem szerokości ekliptycznej do i analogicznie ostatni bok jest dopełnieniem deklinacji do kąta prostego.
Przenosząc naszą uwagę z boków na kąty wewnętrzne trójkąta nietrudno zauważyć, żę kąt przy biegunie niebieskim jest rektascensją powiększoną o kąt prosty, natomiast kąt przy biegunie ekliptycznym to dopełnienie długości ekliptycznej do . Z tak wyznaczonymi miarami kątów i boków można się zabrać za przeliczanie współrzędnych. Zakładając, że początkowo dane nam są deklinacja oraz rektascensja, możemy zapisać twierdzenie cosinusów w celu wyznaczenia szerokości ekliptycznej:
które po uproszczeniu przyjmuje postać
Wartość współrzędnej można następnie użyć do wyliczenia długości ekliptycznej na podstawie twierdzenia sinusów
Wyznaczenie wzorów na transformację współrzędnych w odwrotną stronę pozostawiamy czytelnikowi jako proste ćwiczenie.
Wyprowadzone przekształcenia pokazują, że podróżowanie pomiędzy układami współrzędnych wymaga jedynie skonstruowania prawidłowego trójkąta paralaktycznego i zastosowania odpowiednich twierdzeń trygonometrii sferycznej. Dzięki takim manewrom obserwatorzy z różnych miejsc na Ziemi z różnymi montażami teleskopowymi mogą z łatwością przekazywać sobie informacje na temat położenia wybranych obiektów na sferze niebieskiej.
Zadania
Zadanie 1
Znaleźć azymut oraz odległość zenitalną gwiazdy (Kapella) o deklinacji
i rektascensji
w Katowicach (
) dla czasu gwiazdowego
.
Zadanie 2
Franek, prowadząc regularne obserwacje, zauważył, że azymut wschodu Słońca zmienia się w ciągu jednego roku o . Jaka jest szerokość geograficzna z której prowadzi swoje obserwacje. Można pominąć rozmiary tarczy Słońca oraz zjawisko refrakcji.
Rozwiązania
Zadanie 1
Znając rektascensję oraz czas gwiazdowy bezpośrednio wyznaczyć można kąt godzinny co po zamianie na odpowiednie jednostki wynosi
Wykorzystując teraz wyprowadzony wzór na wysokość jako funkcję deklinacji, kąta godzinnego oraz szerokości geograficznej otrzymujemy wynik
zatem odległość zenitalna to
Na koniec, wykorzystując wszystkie podane informacje oraz wyznaczoną wysokość, obliczyć możemy azymut Kapelli
co daje końcową wartość .
Zadanie 2
Deklinacja Słońca w ciągu roku przyjmuje graniczne wartości oraz
podczas odpowiednio przesilenia zimowego oraz letniego. Są to wartości symetryczne względem
.
Z wyprowadzonych zależności dla azymutu wschodu Słońca wiemy także, że
a zatem graniczne wartości azymutu będą symetrycznie usytuowane względem geograficznego wschodu, to jest . Oznacza to, że maksymalny azymut wynosi
i jest to azymut wschodu Słońca w trakcie przesilenia zimowego. To właśnie wtedy Słońce wschodzi najdalej od bieguna niebieskiego północnego na półkuli północnej, a najbliżej bieguna niebieskiego południowego na półkuli południowej. Możemy to od razu wykorzystać do wyznaczenia szerokości geograficznej
a zatem albo, ze względu na parzystość funkcji cosinus
.
- Astronomia Ogólna, E.Rybka
- Materiały Mateusza Krakowczyka