Gdy patrzy się w nocne niebo, ciężko nie pomyśleć: jakie to wszystko wielkie. A mimo tego, to co widać gołym okiem na niebie, jest tylko wycinkiem naszej galaktyki, nie mówiąc już o całym wszechświecie. Wiadomo, że gwiazdy łączą się w galaktyki o ciekawych strukturach, ale czy jest w tym jakiś większy porządek? Okazuje się, że tak.

Artykuł napisał Kamil Ciebiera

Wielkoskalowe struktury

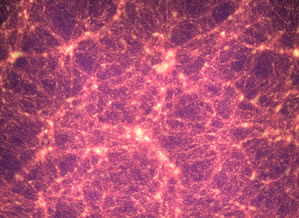
Astronomom udało się zmapować duże kawałki obserwowalnego wszechświata, i to, co pokazały obserwacje to to, że materia we wszechświecie układa się we włókna, między którymi są wielkie pustki.

Paul Bourke and Alexander Knebe, Swinburne University of Technology

Takie rozłożenie powstało na skutek pierwotnych nierówności w gęstości materii po Wielkim Wybuchu, przez które materia zaczęła gromadzić się w gęstsze obłoki. Gdyby nie to, wszechświat byłby tylko wielką pustką pełną pyłu, wszędzie wyglądającą tak samo.

Według zasady kopernikańskiej wszechświat na odpowiednio dużej skali powinien wyglądać wszędzie tak samo i obecnie uznaje się, że włókna są już na tym poziomie. A może istnieje coś ciekawego, ale trochę mniejszego? Odpowiedź brzmi: tak. Najbardziej znane duże struktury to wielkie klastry galaktyk: Great Attractor i Great Wall, ale są też wielkie „pustki”, miejsca, gdzie jest bardzo mało materii. Jedną z największych jest Boötes void, czasami nawet nazywana „wielką nicością”

Ciemna materia i krzywe rotacji galaktyk

Może jednak trzeba przyjrzeć się czemuś mniejszemu. Weźmy galaktyki, są wystarczająco duże na potrzeby tego artykułu. Okazuje się, że od 1884 już coś z nimi nie grało. Gwiazdy poruszały się w nich dużo szybciej, niż wynikałoby to z masy widzialnej w galaktyce materii.

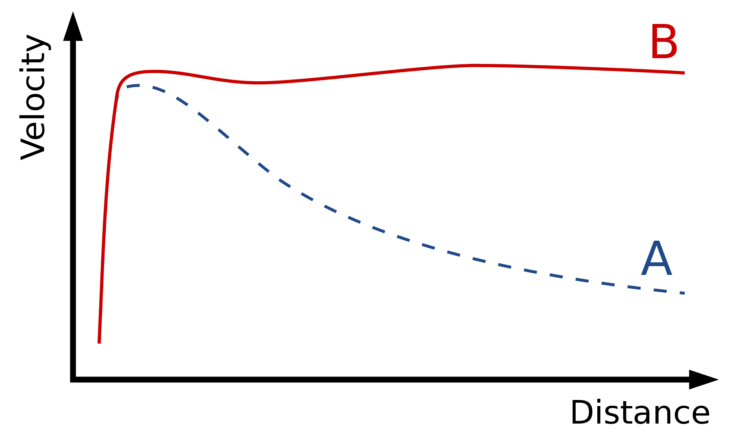
Początkowo przypuszczano, że po prostu większość gwiazd jest zbyt ciemna, żeby je zauważyć, ale gdy nie udał się tego potwierdzić, tę brakującą materię nazwano ciemną materią. Pierwszych dobrych pomiarów ilości ciemnej materii dokonali Vera Rubin, Kent Ford, i Ken Freeman, którzy w latach siedemdziesiątych XX wieku badali krzywe rotacji gwiazd w galaktykach. Takie krzywe pokazują zależność między prędkością orbitalną gwiazd w galaktyce a ich odległością od centrum.

Na obrazku poniżej krzywa A to teoretyczna krzywa gdyby w galaktyce nie było ciemnej materii, natomiast krzywa B jest wyznaczona obserwacyjnie. Według pomiarów około 85% masy w galaktykach jest niewidoczna i oddziałuje ze światem niemal wyłącznie przez siłę grawitacji. Dalej nie wiemy, czym ta materia jest. Obecnie zgaduje się, że są to np. MACHOS (massive compact halo objects), czyli zwykła materia tylko skompresowana w małych nieświecących obiektach, albo WIPMS (Weakly Interactive Massive Particles), czyli egzotyczna materia, która oddziałuje tylko grawitacyjnie.

PhilHibbs, Wikimedia

Soczewkowanie grawitacyjne

Jednym z obecnych sposobów na mierzenie ilości ciemnej materii jest soczewkowanie grawitacyjne. Zgodnie z Ogólną Teorią Względności, światło powinno być zakrzywiane przez masywne obiekty, takie jak galaktyki lub gromady galaktyk. Sprawia to, że obiekt, który normalnie byłby przez taką galaktykę zasłonięty, może być widoczny, ale w innym miejscu na niebie (a czasem nawet być widoczny w kilku kopiach tak jak na obrazku). Znając rozmiary i masę galaktyki można policzyć, jak bardzo ugina się światło. Czasami obiekt może zostać rozciągnięty i być widoczny jako pierścień wokół soczewki, ten efekt nazywa się pierścieniem Einsteina.

photojournal.jpl.nasa.gov

Zadania

1. W pewnej galaktyce gwiazdy na obrzeżach poruszają się około 2 razy szybciej, niż wynikałoby to z masy świecącej materii. Jaki jest stosunek ciemnej materii do zwykłej w tej galaktyce?
2. Zgodnie z Teorią względności punktowe ciało o masie M ugina promień światła przechodzący w odległości b od tego ciała o kąt równy: . Oblicz, ile będzie wynosił ten kąt, jeżeli ciałem jest Słońce, a promień przechodzi tuż nad powierzchnią Słońca. Potrzebne dane wyszukaj samodzielnie.

Zadanie 2 pochodzi z „Kącik olimpijczyka” – Model grawitacyjnej soczewki punktowej

Rozwiązania zadań

Zadanie 1

Przybliżając ruch gwiazdy wokół galaktyki ruchem po okręgu, otrzymujemy, że siła grawitacji pełni rolę siły dośrodkowej, więc przyspieszenie grawitacyjne musi być równe dośrodkowemu . Porównując je, dostajemy . Jeżeli teraz przez  oznaczymy teoretyczną prędkość gwiazdy, to dostaniemy, że masa świecącej materii , natomiast całkowita masa galaktyki to . Stąd masa ciemnej materii to  i mamy .

Zadanie 2

Przybliżając Słońce jako ciało punktowe, możemy zastosować wzór z zadania. Dane (przybliżone) , . Po wstawieniu wychodzi radianów, czyli 1,75’’ (sekundy łuku)