Fotometria to dział optyki zajmujący się badaniem cech charakterystycznych dla światła dostrzeganych przez ludzkie oko. Istotne jest tu wrażenie, jakie odnosimy. Dla astronomów fotometria to między innymi porównywanie jasności czy widm gwiazd. W tym artykule przedstawione zostaną elementarne własności światła i zjawiska z nimi związane.

Czym jest światło?

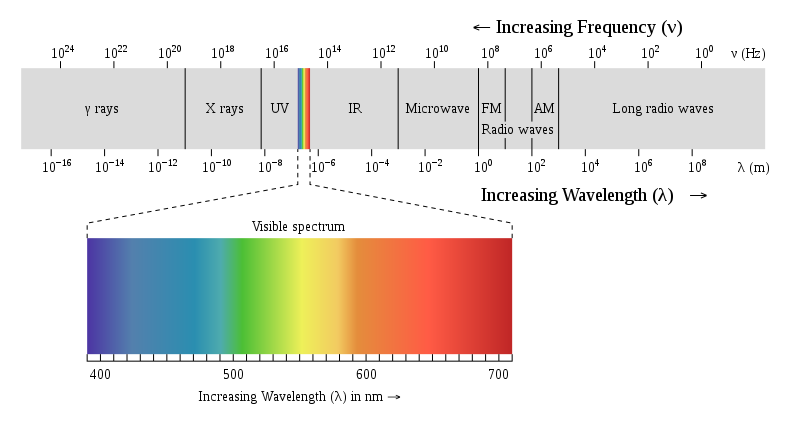
Dla ścisłości na początku powiemy sobie, czym światło w ogóle jest. W naszych rozważaniach będzie ono pewnym rodzajem promieniowania elektromagnetycznego. Sama nazwa światło jest zarezerwowana dla fal elektromagnetycznych o długości fal z zakresu około 400 nm (kolor fioletowy) – 700 nm (kolor czerwony). Niemniej jednak jeśli będziemy mówić o własnościach światła, to zazwyczaj będą one dotyczyć promieniowania z całego zakresu.

Philip Ronan

Graficzna reprezentacja spektrum promieniowania elektromagnetycznego.

Czasami piszemy o falach, czasem o promieniowaniu, a czasem o strumieniu fotonów. Cały czas odnosimy się jednak do tego samego zjawiska, które czasem lepiej potraktować z konkretnej perspektywy, mianowicie jako falę lub jako strumień cząstek. Te dość odmienne sposoby patrzenia na światło nie przeczą sobie. W pewnych warunkach lepiej jest nam modelować światło jako falę, a w innych jako strumień cząstek. Są to równie ważne modele.

O falach i cząstkach

Długo zastanawiano się nad naturą światła i wielokrotnie zmieniała się koncepcja czy światło jest falą (zaburzeniem ośrodka), czy strumieniem cząsteczek. Początkowe odkrycia dotyczyły załamania, dyfrakcji, interferencji i polaryzacji światła. Na podstawie tych obserwacji wyobrażano sobie światło jako falę. Późniejsze odkrycia z dziedzin elektryczności i magnetyzmu wykazały, że światło dobrze pasuje do teoretycznego opisu fal elektromagnetycznych.

Fala to zaburzenie ośrodka. W tym przypadku światło jest rozchodzącym się zaburzeniem pola elektrycznego i magnetycznego. Można je scharakteryzować za pomocą dwóch wielkości: długości fali oraz częstotliwości jej drgań . Długość fali to odległość między dwoma grzbietami lub dolinami fali, natomiast częstotliwość to ilość pełnych drgań wykonywanych przez źródło w jednostce czasu. Te dwie wielkości łączy wzór na szybkość fali, który dla światła możemy zapisać jako:

Gdzie c to prędkość światła w danym ośrodku. W próżni równa się ona 300 000 . Ten wzór jest analogiczny do wzoru na średnią szybkość v w ruchu prostoliniowym: , gdzie s to droga przebyta przez ciało w czasie t. Warto wspomnieć, że w próżni wszystkie rodzaje promieniowania elektromagnetycznego mają tę samą prędkość, natomiast w innych ośrodkach ta prędkość może być inna w zależności od długości takiej fali. Zresztą ta właśnie własność odpowiada za rozszczepienie się światła na pryzmacie.

Późniejsze odkrycia m.in. efektu fotoelektrycznego zasugerowały, że światło jest podobne do strumienia cząsteczek. Nazwano je fotonami. Poruszają się one z prędkością światła c (właściwą dla danego ośrodka i długości fali) i mają zerową masę spoczynkową. To jaką energię niesie ze sobą foton można wyliczyć znając długość fali świetlnej, lub jej częstotliwość. Energię wylicza się ze wzoru:

Gdzie h to stała Plancka równa 6,63 ⋅ 10^-23 J⋅s.

Tak jak dla ujęcia falowego podawaliśmy długość fali, tu możemy się posłużyć energią fotonu. W podziale na konkretne zakresy promieniowania można uwzględnić energię pojedynczych fotonów. W zależności od tego jak duża jest ta energia, możemy wyróżnić różne rodzaje promieniowanie: promieniowanie radiowe, mikrofalowe, podczerwone, widzialne, nadfioletowe, rentgenowskie oraz gamma. Fale radiowe są najdłuższe i niosą najmniejsze energie, a falami gamma nazywamy te najkrótsze i najbardziej energetyczne.

Widzenie ludzkim okiem możliwe jest dlatego, że pewne substancje reagują z promieniowaniem o konkretnych długościach fal. W ludzkim oku są specjalne receptory zwane czopkami i pręcikami, które pod wpływem światła wysyłają określone sygnały do mózgu. Receptory te są najbardziej wrażliwe na kolory czerwony, zielony i niebieski, stąd też wyświetlacze budowane są z pikseli o takich kolorach. Zmieszanie tych kolorów powoduje u nas iluzję kolorów.

Energia światła

Źródła światła razem z promieniowaniem pozbywają się części swojej energii. Moc promieniowania będzie zależała od amplitudy fali, zaś w korpuskularnym ujęciu będzie sumą energii poszczególnych fotonów w danym czasie. W astronomicznych przypadkach często będzie nas interesować całkowita moc gwiazdy lub natężenie dochodzącego do nas światła . Drugi termin dotyczy mocy przypadającej na  w danej odległości. Gdybyśmy otoczyli taką gwiazdę pewną powierzchnią, to moc odbierana przez tę powierzchnię byłaby mocą całkowitą gwiazdy. Możemy przyjąć, że gwiazdy w każdym kierunku emitują taką samą energię, co upraszcza nasze obliczenia do rozważenia sfery o środku w centrum gwiazdy. Tym sposobem uzyskujemy natężenie od gwiazdy o mocy w odległości .

Znając natężenie światła dobiegające od danej gwiazdy na Ziemi oraz odległość do niej jesteśmy w stanie wyznaczyć jej całkowitą moc. Właśnie to pojęcie natężenia kryje się we wzorze Pogsona.

Pęd światła

Mimo, że fotony nie mają masy spoczynkowej możemy policzyć ich pęd i siłę wywieraną na pewne ciało. Zależność ta jest również prawdziwa dla innych cząstek, jednak w ich przypadku chcemy raczej obliczyć długość fali.

Dzięki temu zjawisku działają między innymi żagle słoneczne.

Efekt Dopplera

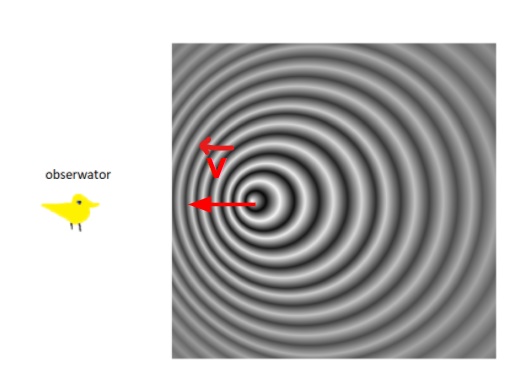
Światło wykazuje własności falowe, więc tak jak na przykład fale dźwiękowe będzie podlegać efektowi Dopplera. Najczęściej jest on ilustrowany za pomocą jadącej karetki na sygnale. Zbliżając się do nas, dźwięk syreny jest zauważalnie wyższy do tego, który słyszymy w chwili gdy pojazd się od nas oddala. Czynnikami określającym zmianę częstotliwości są prędkość źródła fali oraz prędkość odbiornika fali, dla obu jest to prędkość względem ośrodka.

Promieniowanie elektromagnetyczne rozchodzi się w próżni i każdym innym ośrodku, więc sprawy się tu nieco skomplikują. W pewnym uproszczeniu można powiedzieć, że zbliżające się do siebie źródło i odbiorca powodują wzrost początkowe częstotliwości, a ich oddalanie powodują spadek częstotliwości. W astronomii często mówimy o przesunięciu ku czerwieni lub przesunięciu ku fioletowi. Nazwy te znaczą odpowiednio zwiększenie długości fali i zmniejszenie jej.

Jeśli źródło pozostaje w spoczynku względem nas, wtedy odbieramy światło o takiej samej długości i częstotliwości co emitowane. Jeśli źródło światła się do nas zbliża, lub my idziemy w jego kierunku, wówczas widzimy światło o częstotliwości wyższej, niż to emitowane. Mówimy, że obserwujemy przesunięcie ku fioletowi. Analogicznie, gdy źródło oddala się od nas, lub my od niego, widzimy światło o niższej częstotliwości. Mówimy, że obserwujemy przesunięcie ku czerwieni.

Wikipedia, edit: Zuzz

Klasycznie zmianę częstotliwości odbieranego przez nas światła możemy określić, korzystając ze wzoru:

Gdzie to częstotliwość obserwowana, to częstotliwość emitowana, c to szybkość światła w próżni, to szybkość obserwatora, a  to szybkość źródła. Jeśli źródło się do nas przybliża, wówczas używamy znaku „+” i odwrotnie jeśli się oddala „-„. Natomiast jeśli obserwator się zbliża, używamy znaku „-„, a jeśli oddala „+”. Wzór ten ma swoje zastosowania między innymi dla dźwięku.

Dla fal elektromagnetycznych wzór klasyczny nie jest użyteczny, ponieważ prędkość światła, zgodnie ze Szczególna Teorią Względności nie zależy od układu odniesienia. Na odbieraną przez nas częstotliwość fali elektromagnetycznej wpływ ma wyłącznie względna prędkość obserwatora i źródła. Jeśli źródło i obserwator poruszają się względem siebie po prostej, możemy zastosować wzór:

Gdzie i  jest prędkością względną źródła i obserwatora, a  prędkością światła. Jeśli można stosować wzór uproszczony:

Znaku „+” używa się gdy źródło i obserwator się do siebie zbliżają, a „-” gdy się oddalają. Zatem jeśli źródło promieniowania będzie się do nas zbliżać, zaobserwujemy falę o wyższej częstotliwości, czyli przesuniętą ku fioletowi. Natomiast gdy źródło się oddala, odebrane zostanie światło o częstotliwości niższej, czyli przesunięte ku czerwieni.

Istnieją jeszcze inne przyczyny powstawania efektu dopplera np. grawitacja. Fotony wydostające się z gwiazdy wraz z odległością tracą część energii, a wraz z nią wydłuża się ich długość fali. Nazywamy to zjawisko grawitacyjnym przesunięciem ku czerwieni.

Polaryzacja

Światło jest falą poprzeczną, jego kierunek drgania jest prostopadły do kierunku rozchodzenia się. W związku z tym każda fala składowa ma ustalony kierunek drgań. W przypadku zwykłego światła kierunki drgań są w różnych kierunkach. Światło spolaryzowane, to takie, w którym kierunek drgań jest jednolity dla całego docierającego promieniowania. Najprostszym polaryzatorem (w tym przypadku dla fal radiowych lub mikrofal) byłaby siatka z pręcików ustawionych np. poziomo. Wtedy drgania będą mogły się rozchodzić tylko w konkretnym kierunku, a za polaryzator przejdą fale o jednym kierunku drgań.

Inne efekty

W szczególnych warunkach substancje wewnątrz gwiazd mogą emitować nieco inne promieniowanie od spodziewanego. Więcej o emisji w kolejnym artykule, ale na razie można powiedzieć, że konkretne substancje w normalnych warunkach emitują promieniowanie o określonych długościach fal. Wskutek wzrostu temperatury dochodzi do dużej ruchliwości cząstek gazu emitującego światło. Przez to nie dostajemy jednej poprawnej długości fali, a raczej wąski zakres w jej pobliżu. Część promieniowania będzie miała częstotliwość nieco większą, a część mniejszą. Nastąpi wówczas poszerzenie linii widmowych. Podobne zjawisko ma miejsce gdy substancja emitująca światło jest umieszczona w silnym polu elektrycznym lub magnetycznym. Wówczas może nastąpić rozszczepienie promieniowania na parę pobliskich długości fal. Zjawiska te noszą nazwę odpowiednio efektu Starka i efektu Zeemana.

Zadania

Uwaga – do niektórych zadań dobrze się posłużyć jeszcze innymi źródłami.

Zadanie 1

Porównaj natężenie światła dobiegającego od Słońca, Vegi i Betelgezy. Ich jasności to odpowiednio , , . Odległości od Vegi i Betelgezy to 25 i 548 lat świetlnych.

Zadanie 2

Porównaj natężenie światła docierającego na Pluton w peryhelium i aphelium.

Zadanie 3

Wokół słońca w odległości 0,5 AU krąży kometa. Oblicz jakie ciśnienie wywiera na nią Słońce samym promieniowaniem. Albedo komety jest równe 0,1.

Zadanie 4

W widmie pewnej gwiazdy zaobserwowano poszerzenie linii emisyjnych o , przy czym . Znajdź prędkość obrotową gwiazdy na równiku przy założeniu, że oś obrotu jest prostopadła do kierunku obserwatora.

Rozwiązania zadań

Zadanie 1

W tym zadaniu będziemy się posługiwać jednostką natężenia światła słonecznego padającego na ziemię . Dla Vegi wielkość ta będzie wynosić i analogicznie dla Betelgezy. Po podstawieniu danych dostaniemy stosunek światła dobiegającego od tych gwiazd jako . Można zauważyć, że różnica ta jest dość spora i fakt ten odzwierciedlają wielkości gwiazdowe owych gwiazd. Dla Słońca jest to , dla Vegi to  a dla Betelgezy to .

Zadanie 2

Pluton w peryhelium jest w odległości 29,646 AU od Słońca, a w aphelium 48,826 AU. Znajdziemy więc stosunek kwadratów tych promieni.

Stosunek natężenia promieniowania w tych punktach wynosi więc . Widzimy więc, że dla niektórych obiektów różnica w rocznym zaopatrzeniu w energię może być całkiem spora. Podobny efekt jest na Ziemi, jednak różnica odległości w peryhelum i aphelium Ziemi jest znacznie mniejsza. Stosunek ten dla Ziemi wynosi raczej około 7 %.

Zadanie 3

Albedo to stosunek promieniowania odbitego do padającego. Część zaabsorbowanych fotonów przekaże cały swój pęd komecie, natomiast część która się odbije będzie musiała przekazać dwukrotność swojego pędu by jeszcze zawrócić. Siłę z definicji będziemy traktować jako zmianę pędu w czasie, a ciśnienie jako stosunek tej siły do powierzchni. Początkowo załóżmy, że wszyskie fotony są pochłaniane przez ciało.

Skorzystaliśmy z faktów, że  oraz . Nie jest to jeszcze koniec, trzeba bowiem uwzględnić pęd dostarczony przez odbicie części fotonów. Nię będzie to jednak trudne, gdyż otrzymaną wartość ciśnienia nalezy przemnożyć przez , gdzie to wartość albedo. Bierzemy pod uwagę fakt, że pęd wypadkowy będzie sumą pędu fotonów pochłoniętych i odbitych, przy czym odbite działają z dwukrotnie większą siłą. Więc . Dostajemy więc:

Zadanie 4

Wykorzystamy tutaj fakt, że materia z jednej strony gwiazdy była przyspieszona o prędkość obrotową w danym punkcie, a część zosta spowolniona (względem obserwatora). Skorzystamy z faktu, że dla prędkości nierelatywistycznych można zastosować wzór . Wychodzi nam około .

Artykuł powstał we współpracy z Krysią Syty.