Wybierzmy się w hipotetyczną wyprawę po kuli ziemskiej. Stojąc na biegunie północnym, wyruszamy na południe, czyli w dowolną stronę i poruszamy się, nie zmieniając kierunku. Docierając do równika, robimy zakręt o 90°. Poruszamy się następnie dalej prosto, przemierzając 1/4 obwodu Ziemi. Po przebyciu odcinka po równiku ponownie zakręcamy o 90° w tę samą stronę i poruszamy się ponownie prosto. Po ponownym przebyciu czwartej części ziemskiego obwodu znajdujemy się ponownie na biegunie, przybywając z kierunku prostopadłego do kierunku, z którego wyruszyliśmy. Poruszaliśmy się po trójkącie — jedynie po liniach prostych, a kierunek zmienialiśmy jedynie w wierzchołkach, lecz w trójkącie o trzech kątach prostych!

Jak wiadomo, w zwykłym trójkącie suma kątów wewnętrznych wynosi 180°, w naszym zaś 270°. Czy więc w naszym rozumowaniu jest błąd? Podróż odbyła się po trójkącie, ale nie po trójkącie płaskim, bo znajdującym się na powierzchni kuli. Ponieważ nasza dwuwymiarowa przestrzeń jest zagięta, zasady geometrii płaskiej, nie zawsze są zachowane. Możliwe są więc trójkąty o sumie kątów większych od 180°.

Linie geodezyjne

Jeżeli stoimy na Ziemi i rozpoczniemy podróż po linii prostej (czyli bez zmiany kierunku), po przejściu 40 000 km znajdziemy się w tym samym miejscu. Jeśli nie wiedzielibyśmy, o krzywiźnie Ziemi, nasze doświadczenie prowadziłoby do paradoksu. Prosta jest nieskończoną figurą, więc bez zawracania nie moglibyśmy znaleźć się w tym samym miejscu. Poruszaliśmy się po okręgu wielkim sfery — okręgu o promieniu równym promieniowi sfery, który stanowi linię geodezyjną, która w tej geometrii odpowiada prostej, czyli stanowi najkrótszą drogę między obiektami. Linia geodezyjna zwana jest też, zwłaszcza w nawigacji, ortodromą.

Zauważmy, że na sferze nie ma dwóch rozłącznych okręgów wielkich — czyli nie istnieją równoległe linie geodezyjne (z wyjątkiem okręgów przystających). Rozłączne linie zawsze przecinają się w dwóch punktach. Przed dwa dowolne punkty można przeprowadzić jedną ortodromę. Wyjątkiem są dwa punkty antypodyczne (czyli leżące naprzeciwko siebie), gdyż przechodzi przez nie nieskończenie wiele okręgów wielkich. Warto nadmienić, iż linie geodezyjne, choć stanowią rzeczywistą najkrótszą drogę między punktami, na mapach nie stanowią prostych, a krzywe. Mapy są bowiem pewnym odwzorowaniem trójwymiarowej sfery na dwuwymiarową powierzchnię Można je konstruować tak, by były zachowane odległości, powierzchnie lub kąty, jednak nie wszystko na raz. Krzywa, która na mapie Merkatora jest linią prostą, nazywamy loksodromą. Przecina ona wszystkie południki pod tym samym kątem. Choć nie najkrótsza, była często używana w nawigacji morskiej z uwagi na rzadsze zmiany kursu.

Trójkąty sferyczne

Rozważmy trzy nieprzystające okręgi wielkie sfery. Na powierzchni sfery powstało 8 trójkątnych figur, których wszystkie boki są łukami okręgów wielkich. Każda z tych figur to trójkąt sferyczny. Każdy trójkąt sferyczny składa się z 3 kątów wewnętrznych, których suma zawsze jest większa od 180° a mniejsza niż 540°. By omówić właściwości trójkątów sferycznych, porównajmy je w do dowolnego trójkąta płaskiego.

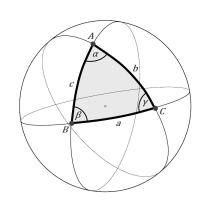Mateusz Krakowczyk

Konstrukcja trójkąta sferycznego.

Właściwości dowolnego trójkąta płaskiego

Rozważmy dowolny trójkąt ABC. Główną właściwością trójkąta płaskiego jest to, że suma wewnętrznych kątów takiego trójkąta zawsze wynosi ona 180°.

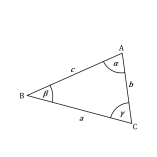Mateusz Krakowczyk

Zgodnie z twierdzeniem sinusów opisanym w poprzednim artykule, bok trójkąta i naprzeciwległy kąt łączy taka zależność:

Z kolei twierdzenie cosinusów pozwala nam na wyliczenie długości boku rozciągniętego na dwóch bokach rozwartych pod danym (przeciwległym do boku) kątem:

Do rozwiązania trójkąta potrzebujemy zazwyczaj 3 niezależnych danych: bok-bok-kąt, kąt-kąt-bok, lub bok-bok-bok. Jedynie w przypadku gdy znamy tylko wartości wszystkich kątów, potrzebujemy czwartego parametru, czyli długości dowolnego boku.

Właściwości dowolnego trójkąta sferycznego

Suma kątów wewnętrznych trójkąta sferycznego ABC nie jest stała, dlatego nie korzystamy z niej podczas rozwiązywania trójkątów sferycznych. Możemy używać jednak poniższego kryterium do sprawdzenia otrzymanych wyników:

Podobnie, jak w przypadku trójkątów płaskich istnieje zależność pomiędzy bokiem a kątem naprzeciwległym, zwana twierdzeniem sinusów trójkąta sferycznego:

Analogicznie do geometrii płaskiej, możemy wyliczyć długość boku powstałego przez rozwarcie dwóch odcinków pod zadanym kątem. Używamy twierdzenia cosinusów trójkąta sferycznego:

Zauważmy, że we wszystkich wzorach występują wyłącznie iloczyny i ilorazy funkcji trygonometrycznych, co sprawia, że rozwiązywanie trójkątów sferycznych nie jest elementarne, jak w przypadku trójkątów na płaszczyźnie. Dlatego w praktyce dążymy do skonstruowania trójkątów szczególnych — np. których wierzchołki odpowiadają pewnych charakterystycznych punktów na niebie, lub prostokątnych, których rozwiązywanie jest znacznie prostsze.

Jednoprostokątny trójkąt sferyczny

Przyjmijmy teraz i rozpiszmy podstawowe wzory danego trójkąta. Ponieważ:

Wzór sinusowy uprości się do:

Natomiast cosinusowy dla „przeciwprostokątnej”:

Otrzymany wzór to sferyczny odpowiednik twierdzenia Pitagorasa. Z powyższych równań wynika, że znając dwa dowolne boki trójkąta jednoprostokątnego, możemy swobodnie rozwiązać dany trójkąt, korzystając wpierw z równania cosinusowego wyliczając trzeci bok, następnie korzystając z równania sinusowego, możemy wyliczyć pozostałe kąty wewnętrzne.

Wieloprostokątne trójkąty sferyczne

Ponieważ suma kątów wewnętrznych w trójkącie sferycznym jest większa od 180◦, możliwe są trójkąty o dwóch lub trzech kątach prostych. Trójkąt dwuprostokątny jest zawsze równoramienny, a trzeci bok co do długości równy kątowi pomiędzy dwoma pozostałymi bokami:

Jeśli trójkąt jest trójprostokątny, jego boki i kąty są równe zawsze 90° i stanowi on krawędź oktantu sfery, czyli wycinka powstałego przez podzielenie sfery prostopadłymi płaszczyznami na 8 równych części. Opisana we wstępie do rozdziału podróż wędrowca, odbywała się właśnie po takim trójkącie.

Równanie okręgu wielkiego

Korzystając z wprowadzonego układu współrzędnych, każdy okrąg wielki posiada pewne równanie definiujące, które podobnie jak równanie prostej na płaszczyźnie po zwala określić, czy zadany punkt leży na rozważanym okręgiem.

Rozważmy pewien sferyczny układ współrzędnych . Każdy okrąg, przecina równik w dwóch punktach, zwanych węzłami. Węzeł, dla którego współrzędna rośnie, gdy poruszamy się zgodnie z kierunkiem wzrostu współrzędnej , nazywamy wstępującym, natomiast przeciwny, dla którego  maleje zstępującym.

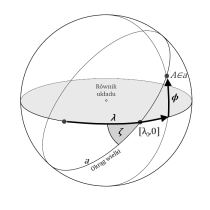Mateusz Krakowczyk

Współrzędne węzła wstępującego określamy jako . Okrąg taki przecina równik pod pewnym kątem . Kąt ten jest równy również wartości bez względnej maksymalnej i minimalnej wartości współrzędnej punktów leżących na tym okręgu. Napiszmy równanie takiej prostej:

Zadania

1. Zakładając, że Ziemia jest idealną kulą, oblicz odległość (długość ortodromy) z Warszawy do Greenwich. Współrzędne tych miejsc to kolejno 52° 13′ 56″ N, 21° 0′ 30″ E oraz 51° 28′ 48″ N, 0° 0′ 0″ E. Załóż, że promień Ziemi wynosi 6 371 km.
2. Przez teleskop widzisz obszar, który na niebie ma średnicę 1,3°. Czy jesteś w stanie zobaczyć jednocześnie Sheliak  oraz mgławicę Pierścień? Potrzebne dane zdobądź sam.

Rozwiązania

Zadanie 1

Na początku stwórzmy trójkąt sferyczny z trzech punktów — G dla Greenwich, W dla Warszawy, oraz B dla bieguna północnego. Szukanym kątem będzie ten, który odpowiada odcinkowi GW na sferze. Mamy wszystkie dane potrzebne nam do użycia twierdzenia cosinusów dla sfery.

W obliczeniach użyliśmy kątów , oraz . Po podstawieniu danych uzyskujemy cosinus kąta między tymi miastami. Z tego wyliczamy kąt (funkcją arc cos), a następnie odległość . Uzyskana odległość to około 1440 km.

Zadanie 2

W tym zadaniu posłużymy się układem równikowym równonocnym, gdyż w porównaniu do układu horyzontalnego lub równikowego godzinnego, współrzędne właściwie nie zmieniają się w czasie (a przynajmniej ten ruch będzie pomijalny). Znajdujemy więc rektascensję oraz deklinację obu obiektów. , oraz , . W tym zadaniu skonstruujemy trójkąt o wierzchołkach w punktach B (biegun północny), P (mgławica Pierścień) oraz S (Sheliak). Obliczamy , oraz . Ważne jest, aby pamiętać, że minuty z rektascensji oraz minuty kątowe to nie ta sama jednostka.

Po wstawieniu liczb do równania otrzymujemy około 0,8°. Oznacza to, że dysponując teleskopem o podanych własnościach, będzie można zobaczyć jednocześnie oba te obiekty. Oczywiście mamy tu na myśli geometryczną możliwość. Pozostaje jeszcze kwestia jasności, przez którą najprawdopodobniej będziemy mieć problem z dostrzeżeniem obiektu.

Współautorem artykułu jest Michał Stefanik.