Kiedy popatrzy się na nocne niebo, łatwo można zauważyć, że nie wszystkie gwiazdy mają tę samą jasność. Niektóre są bardzo jasne, inne są ledwo widoczne. Powody, dla których gwiazdy się różnią, intrygowały astronomów od starożytności. Dziś nie tylko znamy przyczyny takich różnic, ale potrafimy wiele powiedzieć o gwieździe, której jasność znamy.
Artykuł napisał Kamil Ciebiera
Wielkości gwiazdowe
Nad problemem sklasyfikowania gwiazd na podstawie ich jasności myśleli już starożytni Grecy. Jedno z pierwszych rozwiązań zaproponował Hipparch, który postanowił sklasyfikować gwiazdy według ich widocznego rozmiaru, nadając im orientacyjne kategorie od 1 (największe) do 6 (najciemniejsze). W ten sposób powstała skala wielkości gwiazdowej, w której jednostką było magnitudo (od greckiego magnitude – wielkość). Skalę tą w swoim Almageście spopularyzował Ptolemeusz i tak stała się oficjalną skalą do mierzenia jasności gwiazd. Przez długi czas astronomowie uważali, że te różnice w jasności wynikają naprawdę z różnicy rozmiarów, dlatego też pierwsze próby uściślenia tej klasyfikacji polegały na próbach badania rozmiarów kątowych gwiazd, jednak wprowadzenie teleskopów pokazało, że nie tędy droga. Metodę klasyfikacji gwiazd doprecyzował dopiero Norman Pogson, który w 1856 zaproponował skalę logarytmiczną z 3 założeniami:
- Pary gwiazd o równej różnicy magnitudo mają równe ilorazy natężeń
- Gwiazdy o różnicy magnitudo 5 mają iloraz natężeń równy 100
- Wega ma 0 magnitudo.
Z tych założeń można wyprowadzić bardziej znany wzór Pogsona:
Gdzie ,
– wielkości gwiazdowe obiektów 1 i 2, a
,
– natężenia światła od obiektów 1 i 2. Minus bierze się z tego, że skala jest odwrócona (im mniejsze magnitudo, tym większe natężenie).
Wprowadźmy teraz ważne pojęcia:
Wielkość absolutna – wielkość gwiazdowa danej gwiazdy, gdy jest ona obserwowana z odległości 10 pc (dla Słońca wynosi 4.83m). Czasami mówi się o niej również w odniesieniu do obiektów Układu Słonecznego, wtedy jest to ich jasność z odległości 1 AU.
Dzięki niej jesteśmy w stanie, znając jasność obserwowaną danej gwiazdy, obliczyć odległość do niej ze wzoru:
Gdzie m to jasność obserwowalna, M to jasność absolutna a d to odległość w parsekach.
Wielkość bolometryczna – wielkość gwiazdowa uwzględniająca całe promieniowanie gwiazdy.
W odróżnieniu od zwykłej wielkości gwiazdowej, która uwzględnia promieniowanie widzialne, ta bardziej nadaje się do porównywania mocy promieniowania gwiazd, które mają różne temperatury. Dla ludzkiego oka gwiazdy inne niż Żółte mogą wydawać się ciemniejsze, bo ich promieniowanie ucieka poza nasz zakres widzenia. 0 w jasności bolometrycznej jest zdefiniowane jako bolometryczna jasność absolutna gwiazdy o mocy promieniowania 3,0128 x 1028. Dla porównania absolutna jasność bolometryczna Słońca wynosi 4,74m. Różnicę między jasnością obserwowalną a bolometryczną nazywa się poprawką bolometryczną (BC), dostajemy wtedy zależność , gdzie
i
to odpowiednio jasność bolometryczna i obserwowalna.
Wykresy jasności
Na nocnym niebie gwiazdy wyglądają, jakby migotały. To niestety jest tylko złudzenie, ale niektóre gwiazdy naprawdę zmieniają swoją jasność. Takie gwiazdy (poza okazjonalnymi supernowymi z czasów starożytnych) zaczęto odkrywać dopiero po wynalezieniu teleskopów, m.in. Mira Ceti i Algol są gwiazdami okresowo zmiennymi.
Gwiazdy zmienne dzielimy na dwie kategorie:
Gwiazdy zmienne fizycznie to gwiazdy, które zmieniają swoją jasność na skutek zmian zachodzących w gwieździe. Są to te gwiazdy, w których rzeczywiście coś się zmienia, na przykład okresowo robią się większe, lub wybuchają jako supernowe.
Gwiazdy zmienne geometrycznie to te, które nie zmieniają swojej jasności samej w sobie, ale ich obserwowana jasność zmienia się pod wpływem zmiany ich orientacji względem obserwatora, na przykład są to gwiazdy zaćmieniowe lub gwiazdy, w których niektóre części świecą ciemniej niż inne.
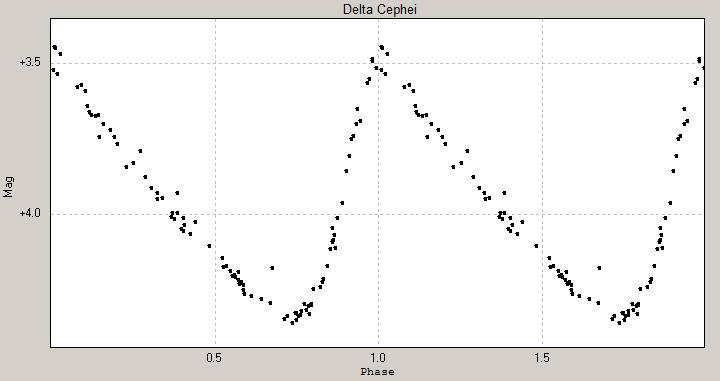
Wykres zmiany jasności dla gwiazdy Delta Cephei.
Ciekawymi gwiazdami zmiennymi fizycznie są cefeidy, ponieważ ich okres jasności pozwala dość dokładnie poznać ich jasność, dzięki czemu działają jak tzw. świece standardowe, swoiste kosmiczne latarnie pozwalające określić odległości w galaktyce. Przykładowo, jeżeli gwiazda jest cefeidą standardową, to odległość od niej można obliczyć ze wzoru:
Gdzie P to okres zmiany jasności gwiazdy w dniach, d to odległość w parsekach a V i I to odpowiednio średnia jasność obserwowalna w świetle widzialnym i podczerwieni. Wszystkich zainteresowanych olimpiadą od razu uspokoję, tego wzoru nie trzeba się uczyć na pamięć.
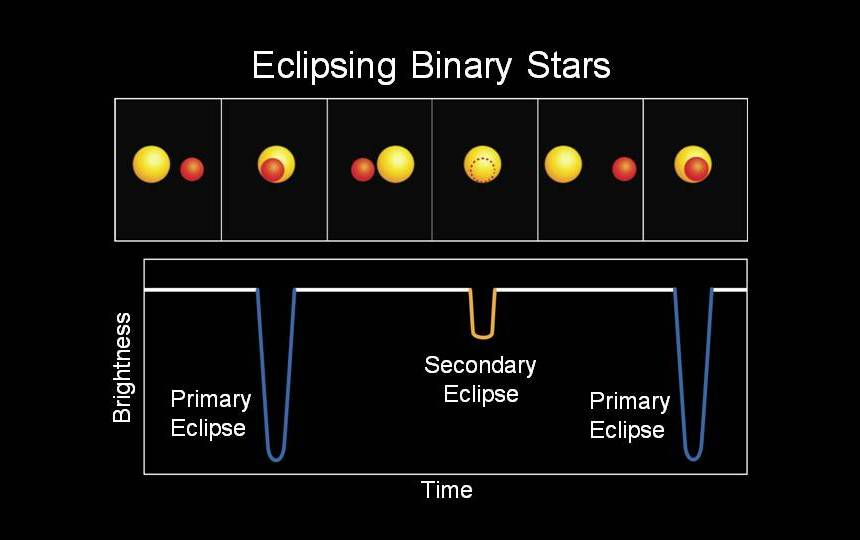
Wykres zmiany jasności dla układu gwiazd podwójnych.
Natomiast wykresy jasności gwiazd zaćmieniowych są w stanie dużo powiedzieć o relacji między gwiazdami w układzie podwójnym, między innymi o stosunku temperatur ich powierzchni lub okresie ich obrotu, ale o tym więcej na układach podwójnych. Taki wykres składa się z dwóch spadków jasności: minima głównego (ciemniejsza gwiazda zasłania jaśniejszą) i wtórnego (jaśniejsza zasłania ciemniejszą).
Przykładowe zadania
- Z założeń podanych przez Pogsona wyprowadzić wzór (1).
- Ze wzoru (1) wyprowadzić wzór (2).
- W pewnym układzie podwójnym składnik A układu na jasność obserwowaną 0,01m, a składnik B 1,33m. Jaka jest jasność obserwowalna tego układu?
- Cefeida klasyczna o okresie zmienności 4 dni ma średnią obserwowalną jasność 1,98m w świetle widzialnym. Znajduje się ona 447 lat świetlnych od Ziemi. Jaka jest jej jasność absolutna w podczerwieni?
- Zmierzono jasność pewnego białego karła w trzech filtrach: B = 18,11 mag, V = 18,08 mag, I = 17,89 mag. Wiedząc, że dla typowej materii międzygwiazdowej stosunek ekstynkcji do nadwyżki barwy wynosi:
i
, oblicz stosunek
.
Wskazówka: nadwyżka barwy, to różnica między obserwowanym (poczerwienionym) kolorem obiektu a prawdziwym (niepoczerwienionym) kolorem:i
, gdzie:
i
, należy rozumieć jako:
i
.
To zadanie zawiera częściowo rozwiązanie zadania 2 z finału 61 OA, jeżeli ktoś chce je zrobić bez podpowiedzi to można je znaleźć na stronie OA.
Rozwiązania
Zadanie 1
Niech i
to jasności obserwowane dwóch obiektów, a
i
to odpowiadające im natężenia światła. Z założenia (2) wiemy, że gdy
to
.
Zastanówmy się, jak to powinno wyglądać dla . Mamy wtedy
i z założenia (1) wiemy, że wszystkie ułamki po lewej są równe. Czyli
. Podobne rozumowanie możemy przeprowadzić dla każdej wartości x,
dostając wzór
, minus bierze się właśnie z odwrócenia skali (dla matematyków: formalnie można to napisać dla x wymiernych i potem należy uciąglić). Teraz wystarczy zlogarytmować stronami, aby otrzymać wzór
Zadanie 2
Niech to natężenie światła obserwowane a
to natężenie światła w odległości 10 pc od obiektu. Jeżeli L to moc promieniowania obiektu, to możemy napisać
,
, czyli
. Podstawiając to do wzoru (1) i korzystając z własności logarytmów szybko dostajemy
.
Zadanie 3
Zastanówmy się najpierw, jak to policzyć. Ponieważ skala jasności jest względna, trzeba wybrać jakieś ciało, z którym cały układ porównamy. Najlepiej będzie wybrać któreś z podanych ciał, powiedzmy, że będzie to składnik A.
Przez oznaczmy jasność obserwowaną A,
jasność obserwowaną B i przez
jasność całego układu, a przez
,
,
odpowiednie natężenia.
Wiemy, że natężenia się sumują oraz, że prawdziwe jest równie:
. Natomiast policzyć potrzebujemy:
Zatem musimy te równania przekształcić:
Wystarczy już tylko podstawić, wychodzi . Możemy teraz sprawdzić wynik, wiedząc, że dane dotyczyły układu Alpha Centauri, wynik zgadza się z rzeczywistymi pomiarami.
Zadanie 4
Żeby to zadanie rozwiązać, najpierw policzmy średnią obserwowaną jasność w podczerwieni. Wystarczy przekształcić wzór (3) do postaci:
Z czego po podstawieniu wychodzi . Teraz wystarczy skorzystać z wzoru (2) żeby dostać
.
Zadanie 5
Jest to jedno z tych zadań na Olimpiadzie Astronomicznej, które nie jest bardzo trudne, ale sprawdza umiejętność wykorzystania nowych wiadomości, w tym przypadku nadwyżki barwy. Najpierw ciut o ekstynkcji: ponieważ w przestrzeni międzygwiazdowej znajduje się pył, to część światła z gwiazdy jest po drodze pochłaniana. Ponieważ czerwone fale są pochłaniane słabiej, mówi się że światło jest “poczerwienione” (tego zjawiska nie należy mylić z redshiftem, o tym więcej na kosmologii). Ekstynkcji używa się bardzo prosto, zachodzi zależność , gdzie
to jasność obserwowana w filtrze,
to teoretyczna obserwowana jasność niepoczerwieniona, a
to ekstynkcja w wybranym filtrze. Gdy już to wszystko wiemy, zadanie staje się dość proste (a przynajmniej ta jego wersja). Rozpisujemy z definicji
i
.
Teraz zauważmy, że gdy od pierwszego równania odejmiemy drugie to po lewej stronie z definicji dostaniemy , czyli mamy:
Zainteresowani mogą spróbować teraz rozwiązać zadanie 2 z finału 61 OA, mam nadzieję że ten wynik pomoże przy rozwiązywaniu.
- Eugeniusz Rybka: Astronomia Ogólna. Warszawa, Wydawnictwo Naukowe PWN, 1983.
- Jerzy Marek Kreiner: Astronomia z Astrofizyką. Wydawnictwo Naukowe PWN, 1992.