Gwiazdy od początku swojego życia, świecą korzystając ze swoich zasobów paliwa. Drogą fuzji termojądrowej spalają kolejno wodór, hel i inne pierwiastki. Jednak łańcuch przemian zatrzymuje się na żelazie, gdyż dalsze przemiany są energetycznie nieefektywne. Co dzieje się z ogromną kulą świecącej materii, gdy zabraknie w niej energii do podtrzymania życia?

Materia zdegenerowana

Gwiazdy mogą utrzymywać stabilną formę dzięki równowadze dwóch sił. Grawitacja stara się ścisnąć całą materię gwiazdy, jednak jest powstrzymywana przez fuzję termojądrową, dzięki której we wnętrzu gwiazdy powstaje ciśnienie stabilizujące układ. Jednakże do fuzji potrzebne jest paliwo, które ostatecznie musi się wyczerpać. Następuje wtedy koniec równowagi i gwiazda zaczyna się kurczyć pod wpływem grawitacji. Jednak podczas ściskania gwiazdy, grawitacja musi się zmierzyć z innymi siłami, które się jej przeciwstawią, a to, na którym etapie zostanie powstrzymana, zależy praktycznie wyłącznie od masy gwiazdy.

Źródłem sił powstrzymujących grawitację po ustaniu fuzji termojądrowej jest zakaz Pauliego. Dotyczy on fermionów, czyli grupy cząstek elementarnych, do której należą m.in. elektrony, a także kwarki budujące protony i neutrony. Zakaz Pauliego mówi, że dwa fermiony nie mogą jednocześnie zajmować tego samego stanu kwantowego. Zasada ta jest najlepiej widoczna w konfiguracjach elektronowych pierwiastków. Elektrony w atomach dążą do zajęcia jak najniższych poziomów energetycznych, jednak nie mogą wejść na miejsce zajmowane już przez inne elektrony i dlatego są zmuszane do pozostawania na wyższych powłokach.

Jednak wpływ zakazu Pauliego nie kończy się na konfiguracjach elektronowych, ale jest kluczowym elementem przy tworzeniu się tzw. materii zdegenerowanej. Jeżeli będziemy ściskać gaz, tak jak grawitacja ściska gwiazdę, w końcu dotrzemy do momentu, w którym elektrony zajmą wszystkie najniższe stany energetyczne i nie będzie już miejsca na kolejne. Dalsze próby ściskania gazu okażą się nieskuteczne z powodu ciśnienia wywołanego przez zdegenerowane elektrony. Ściśniętą w ten sposób materię nazywamy materią zdegenerowaną.

Zakaz Pauliego nie musi dotyczyć jedynie elektronów, ale również np. neutronów. Gdybyśmy próbowali ściskać materię zbudowaną z samych neutronów, również natrafilibyśmy na barierę. Powstała w ten sposób materia zdegenerowana miałaby gęstość podobną do gęstości jądra atomowego, czyli ok. 10¹⁷ [kg/m³].

Białe karły i gwiazdy neutronowe

To właśnie zakaz Pauliego jest źródłem ciśnienia powstrzymującego gwiazdę od nieskończonego zapadania się w sobie po ustaniu fuzji. Dla gwiazd o małych masach, w tym dla naszego Słońca, ciśnienie zdegenerowanych elektronów będzie wystarczające do utrzymania równowagi. Obiekty powstałe z takich gwiazd są nazywane białymi karłami.

Dla przykładu: fuzja dla naszego Słońca ustanie na etapie tworzenia węgla i tlenu (w fazie czerwonego olbrzyma) i to właśnie te pierwiastki będą tworzyć białego karła, którego wielkość będzie porównywalna do rozmiarów Ziemi.

Gęstości białych karłów wahają się pomiędzy 10⁶, a 10¹⁰ [kg/m³]. Łyżeczka białego karła o średniej gęstości 10⁸ [kg/m³] ważyłaby pół tony. Promień białego karła jest zależny od jego składu oraz masy, jednak dla karłów zbudowanych z takiej samej materii, zachodzi następująca zależność pomiędzy promieniem, a masą:

(1)  

By user:AllenMcC. (original jp0g file)user:Trex (vectorization)user:Incnis Mrsi (design tweaks) - File:WhiteDwarf mass-radius fr.svg, CC BY 3.0,

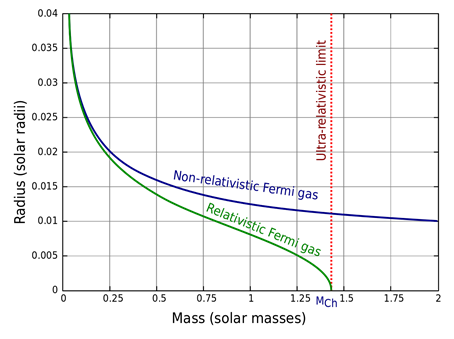
Grafika przedstawia zależność promienia do masy białego karła. Gaz Fermiego jest fizycznym modelem, którym można przybliżyć materię budującą białego karła. Przy uwzględnieniu teorii względności pojawia się graniczna masa, której nie może przekroczyć biały karzeł.

Im bardziej masywny karzeł, tym jego promień jest mniejszy. Jednak masa białego karła nie może być dowolnie duża. Przy zbyt masywnym karle, grawitacja w końcu przezwycięży ciśnienie materii zdegenerowanej i gwiazda zacznie zapadać się dalej. Zakaz Pauliego nie zostanie jednak złamany, energia będzie na tyle duża, że wciśnie elektrony do jąder atomowych, gdzie w wyniku fuzji z protonami utworzą neutrony. Graniczna masa białego karła nosi nazwę granicy Chandrasekhara i wynosi ok. 1,44 masy Słońca. Jednak aby biały karzeł przekroczył tę granicę, masa gwiazdy, z której powstanie musi mieć wynosić ponad 8 mas Słońca, gdyż dla tych gwiazd większość materii zostaje wyrzucona w postaci supernowej przy ustaniu fuzji termojądrowej.

Obiekty, których zapadanie zostało zatrzymane na etapie neutronów, nazywane są gwiazdami neutronowymi. Ich gęstość jest porównywalna z gęstością jądra atomowego, a rozmiary mogą być liczone w kilometrach. Gdyby Ziemię ścisnąć do gęstości gwiazdy neutronowej, jej promień wyniósłby ok. 300 m. Łyżeczka gwiazdy neutronowej ważyłaby 5000 ton, czyli tyle ile około tysiąc słoni.

Z powodu zasady zachowania momentu pędu, gwiazdy neutronowe wirują niesamowicie szybko. Najszybsze potwierdzone gwiazdy neutronowe wykonują nawet kilkaset obrotów na sekundę. Mają one również niezwykle silne pola magnetyczne, nawet 10¹² razy silniejsze od pola ziemskiego. Obiekty o najsilniejszych polach magnetycznych nazywane są magnetarami.

Niektóre gwiazdy neutronowe mogą wysyłać silne wiązki promieniowania elektromagnetycznego ze swoich biegunów magnetycznych. Przy odpowiednim ułożeniu gwiazdy neutronowej wiązki te mogą być odbierane na Ziemi w postaci pulsów. Obiekty, które obserwujemy w ten sposób to pulsary.

Czarne dziury

Podobnie, jak w wypadku białych karłów, tak i dla gwiazd neutronowych istnieje masa, przy której grawitacja przezwycięży ciśnienie neutronów i będzie nadal ściskać gwiazdę. Odpowiednikiem granicy Chandrasekhara dla gwiazd neutronowych jest granica Tolmana-Oppenheimera-Volkoffa (granica TOV), która wynosi ok. 2,3 masy Słońca, jednak dla szybko wirujących gwiazd neutronowych może być wyższa. Masa gwiazdy, z której powstałaby gwiazda neutronowa przekraczająca granicę TOV wynosi 25 mas Słońca. Samo jądro takiej gwiazdy ma masę 3 Słońc.

Hipotetycznie po przełamaniu ciśnienia zdegenerowanych neutronów grawitacja powinna natrafić na jeszcze jedną barierę, czyli zdegenerowane kwarki. Takie hipotetyczne obiekty, składające się z niezwykle mocno ściśniętych kwarków noszą nazwę gwiazd kwarkowych, jednak jak na razie nie potwierdzono ich istnienia obserwacjami.

Jednak nawet dla gwiazd kwarkowych istniałaby granica, po której na drodze grawitacji nie stanęłaby już żadna inna siła. Gwiazda zapadałaby się bez ograniczeń do tzw. osobliwości, czyli nieskończenie gęstego punktu, którego nie da się opisać współczesnymi teoriami fizycznymi.

Osobliwość stanowi centrum czarnej dziury i jest otoczona horyzontem zdarzeń, czyli sferą, zza której nie może wydostać się nawet światło. Każdą czarną dziurę po jej uformowaniu można w całości opisać jedynie za pomocą trzech parametrów: masy, momentu pędu oraz ładunku elektrycznego. Oprócz tych trzech własności czarna dziura nie zachowuje żadnych cech obiektu, z którego powstała.

Rozmiar horyzontu czarnej dziury opisuje promień Schwarzschilda. Dla niewirujących czarnych dziur wynosi on:

(2)  

Wzór ten można naiwnie wyprowadzić ze wzoru na drugą prędkość kosmiczną, jednak prawdziwa natura horyzontu zdarzeń leży w ogólnej teorii względności. Nie chodzi o to, że światło jest za wolne, aby uciec z czarnej dziury, a o to, że czasoprzestrzeń jest tak mocno zagięta, że wewnątrz horyzontu zdarzeń nie istnieje kierunek „na zewnątrz”.

Wzór ten można naiwnie wyprowadzić ze wzoru na drugą prędkość kosmiczną, jednak prawdziwa natura horyzontu zdarzeń leży w ogólnej teorii względności. Nie chodzi o to, że światło jest za wolne, aby uciec z czarnej dziury, a o to, że czasoprzestrzeń jest tak mocno zagięta, że wewnątrz horyzontu zdarzeń nie istnieje kierunek „na zewnątrz”.

Dla wirujących lub obdarzonych ładunkiem elektrycznym czarnych dziur promień Schwarzschilda jest mniejszy i w sytuacji ekstremalnej dąży do:

(3)  

Po powstaniu czarna dziura nie może się już zmienić w nic innego. Przy zderzeniu dwóch czarnych dziur powstanie jedna, jeszcze większa. Jednak nie oznacza to, że czarne dziury są nieśmiertelne. Stephen Hawking próbował opisać zachowanie materii w sąsiedztwie czarnej dziury za pomocą mechaniki kwantowej. Z pracy Hawkinga wynikało, że czarna dziura powinna, na skutek zasady nieoznaczoności Heisenberga, emitować cząstki. Hipotetyczne cząstki emitowane przez czarne dziury noszą nazwę promieniowania Hawkinga.

Jak na razie nie zaobserwowano promieniowania Hawkinga, jednak jeśli istnieje, oznacza to, że czarne dziury powoli wypromieniowują swoją masę. Im mniejsza czarna dziura tym dzieje się to szybciej, jednak i tak jest to bardzo powolny proces. Czarna dziura o masie Słońca potrzebowałaby 10⁶⁴ lat, aby całkowicie wyparować. Dla porównania: wiek wszechświata ma rząd wielkości jedynie 10¹⁰ lat.

Zadania

1. Masa Ziemi wynosi 5,97 ∙ 10²⁴ [kg]. Jaki promień miałby horyzont zdarzeń niewirującej czarnej dziury o masie Ziemi?
2. Z jaką szybkością porusza się punkt na równiku gwiazdy neutronowej o masie 1,5 masy Słońca obracającej się 30 razy na sekundę? Masa Słońca wynosi ok. 2 ∙ 10³⁰ [kg]. Przyjmij, że gęstość gwiazdy neutronowej jest równa gęstości jądra atomowego.

Rozwiązania

Zadanie 1

Promień horyzontu zdarzeń można wyznaczyć korzystając ze wzoru na promień Schwarzschilda.

(4)  

Dla czarnej dziury o masie Ziemi wynosi on około 9 [mm].

Zadanie 2

Pierwszym etapem rozwiązania tego zadania jest znalezienie promienia tej gwiazdy neutronowej. Gęstość jądra atomowego wynosi około 10¹⁷. Masa gwiazdy neutronowej to 2∙10³⁰ [kg]∙1,5 = 3∙10³⁰ [kg]. Korzystając ze wzorów na gęstość oraz objętość kuli można wyznaczyć promień obiektu.

(5)  

Szybkość punktu na równiku gwiazdy neutronowej, to szybkość w ruchu po okręgu o promieniu  z częstotliwością f = 30 [Hz].

(6)  

Podstawiając dane z zadania otrzymujemy szybkość ok. .